Greedy algorithm python github example

Greedy algorithm python github example

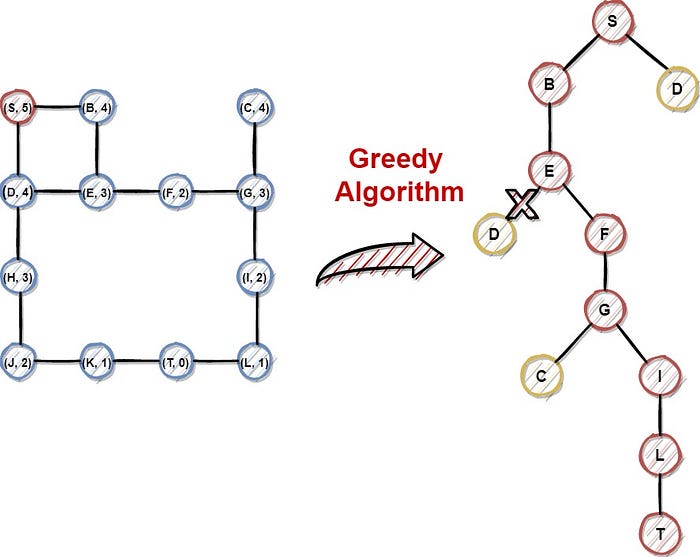
I'll respond in English since that's what you asked for.

Now, let's talk about greedy algorithms in Python and provide a GitHub example. A greedy algorithm is one that makes the optimal choice at each step as it attempts to find the overall optimal solution. It does not necessarily make the best decision at all steps, but it should make a good enough choice to stay on track for finding an optimal solution.

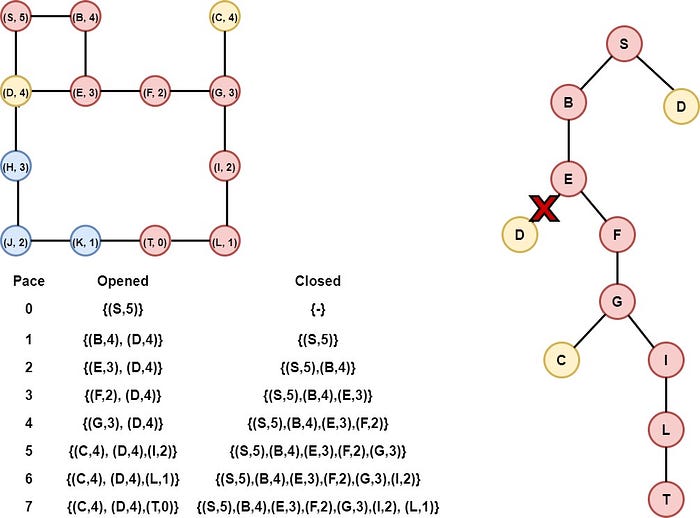
Here's a simple Python example of a greedy algorithm:

Example: Huffman Coding

Huffman coding is a lossless compression scheme that assigns variable-length codes to each symbol in a string. The idea is to assign shorter lengths to more frequent symbols and longer lengths to less frequent symbols, thereby compressing the data more effectively.

In this example, we'll create a simple Huffman coding algorithm using Python:

import heapq
class Node:
def init(self, char, freq):
self.char = char
self.freq = freq
self.left = None
self.right = None
def lt(self, other):
return self.freq < other.freq
def calculate_frequency(chars):
frequency = {}
for char in chars:
if char not in frequency:
frequency[char] = 0
frequency[char] += 1
return frequency
def build_huffman_tree(chars):
frequency = calculate_frequency(chars)
heap = []
for char, freq in frequency.items():
node = Node(char, freq)
heapq.heappush(heap, node)
while len(heap) > 1:
left = heapq.heappop(heap)
right = heapq.heappop(heap)
merged_node = Node(None, left.freq + right.freq)
merged_node.left = left
merged_node.right = right
heapq.heappush(heap, merged_node)
return heap[0]
def build_code(node, prefix):
if node.char:
return {node.char: prefix}
else:
codes = {}
for child in [node.left, node.right]:
codes.update(build_code(child, prefix + '0' if child is node.left else '1'))
return codes
chars = "this is an example for huffman coding"
root = build_huffman_tree(chars)
codes = build_code(root, '')
print(codes)

In this code:

How to run the example:

    python huffman_encoding.py

Key Takeaways:

What is the greedy algorithm in Python?

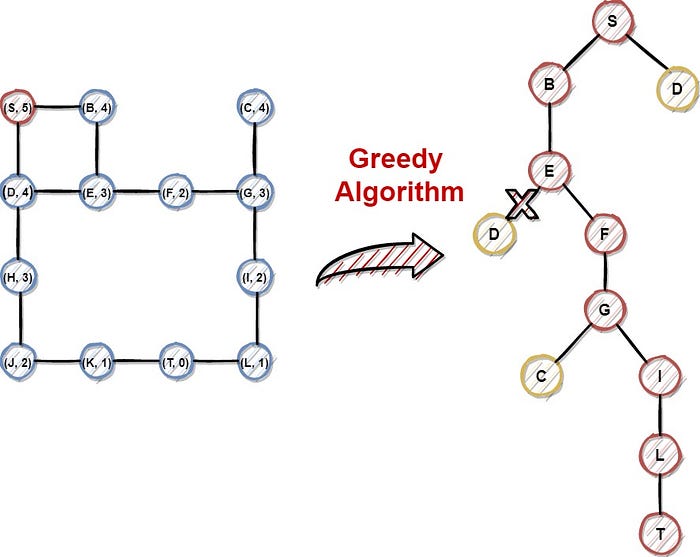
I'd be happy to help!

The Greedy Algorithm is a popular algorithmic approach used to solve problems in computer science. It's called "greedy" because it always chooses the locally optimal solution at each step without considering the global optimum.

In essence, the Greedy Algorithm makes the choice that looks best right now and hopes that these choices will lead to a good overall solution. This strategy is often used when the problem has an optimal substructure, meaning that the problem can be broken down into smaller subproblems, and solving those subproblems optimally leads to the global optimum.

Here's a simple example of how the Greedy Algorithm works:

Coin Changing Problem

Suppose you have a set of denominations for coins (1¢, 5¢, 10¢, etc.) and you need to make change for an amount using these coins. The goal is to find the fewest number of coins needed.

The greedy approach would be to:

This strategy makes sense because you want to use the largest possible coins first, which reduces the number of coins needed overall.

Now, let's see how we can implement the Greedy Algorithm in Python:

Code

Here's a simple implementation of the coin changing problem using the Greedy Algorithm:

def coin_change(coins, amount):
Sort the coin denominations in descending order
coins.sort(reverse=True)
Initialize the result with zeros
result = []
Loop through the coins and add them to the result if possible
for coin in coins:
while amount >= coin:
result.append(coin)
amount -= coin
Return the number of coins used
return len(result)
Example usage
coins = [1, 5, 10]
amount = 12
print(coin_change(coins, amount))  # Output: 2 (2 x 5¢ + 2x 1¢)

In this code:

Conclusion

The Greedy Algorithm is a simple yet powerful approach for solving problems in computer science. By always choosing the locally optimal solution at each step, it can be effective in finding global optima. In this example, we implemented the algorithm to solve the coin changing problem and saw how it efficiently found the fewest number of coins needed.

This strategy has many more applications beyond just making change – think about scheduling, Huffman coding, or even solving knapsack problems!