Python data structures and algorithms Cheat sheet PDF
Python data structures and algorithms Cheat sheet PDF

I'd be happy to help you with that! Here's a comprehensive Python Data Structures and Algorithms Cheat Sheet in PDF format:
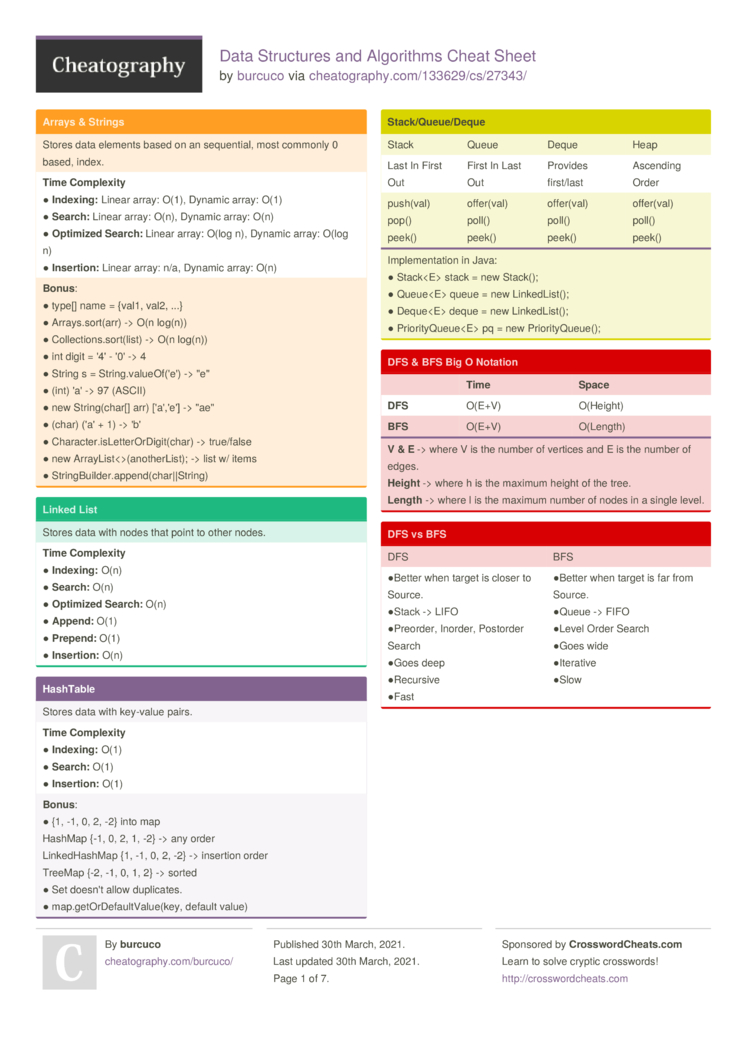
Table of Contents

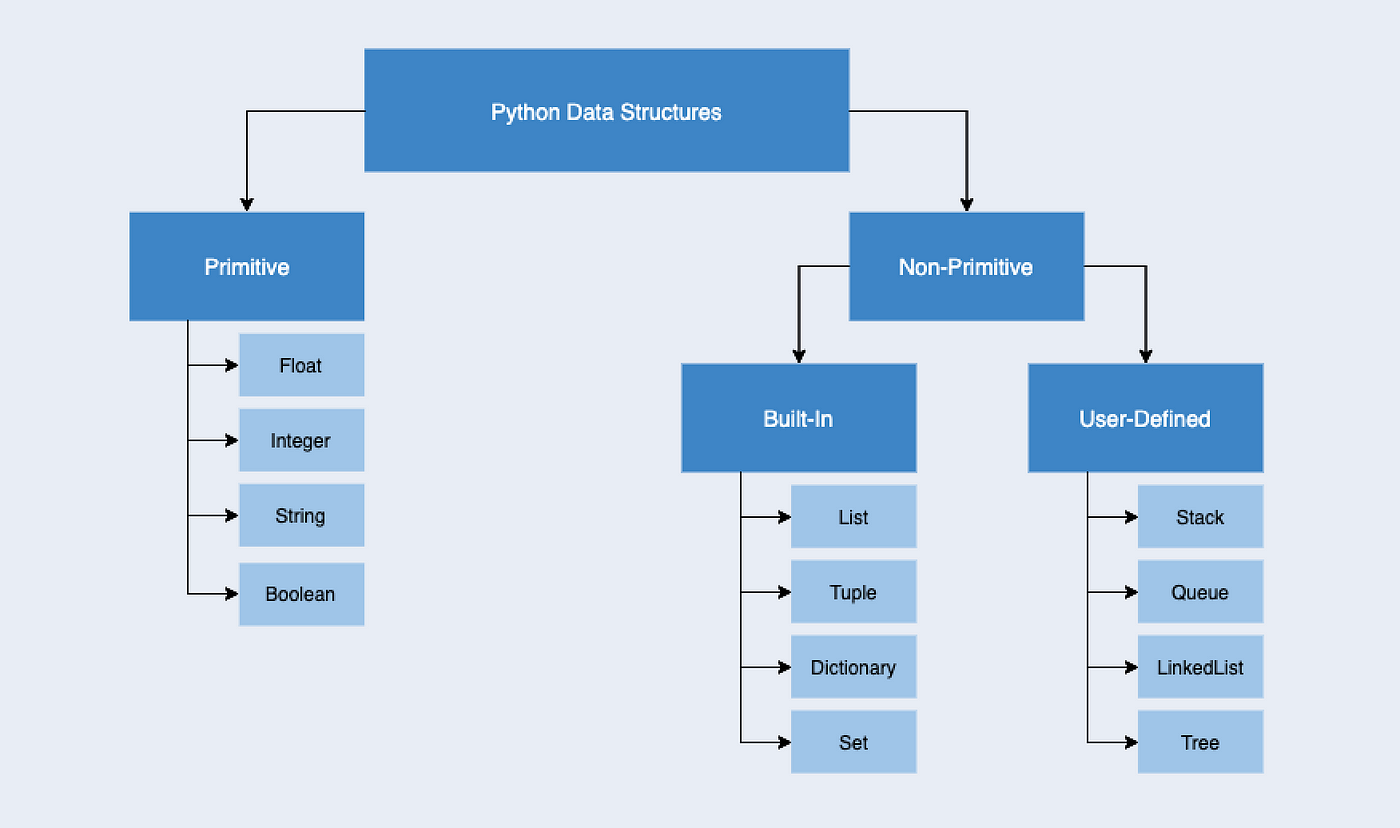
Data Structures
Arrays| Operation | Description |
| --- | --- |
| arr[i] = x | Assigns the value of x to the element at index i |
| arr.append(x) | Adds the element x to the end of the array |
| len(arr) | Returns the length of the array |
| Operation | Description |
| --- | --- |
| node = Node(data) | Creates a new node with the value data |
| head = None | Initializes the head of the linked list to None |
| current = head | Moves to the current node in the linked list |
| next_node = current.next | Retrieves the next node in the linked list |
| Operation | Description |
| --- | --- |
| stack.append(x) | Pushes the element x onto the stack |
| x = stack.pop() | Pops the top element from the stack and returns it |
| Operation | Description |
| --- | --- |
| queue.append(x) | Enqueues the element x |
| x = queue.dequeue() | Dequeues the front element from the queue |
| Operation | Description |
| --- | --- |
| root = Node(data) | Creates a new node with the value data as the root of the tree |
| left = right = None | Initializes the left and right children to None |
| parent.left = child | Sets the left child of the parent node to the child node |
| Operation | Description |
| --- | --- |
| trie.insert(word) | Inserts a word into the trie |
| word = trie.search() | Searches for a word in the trie and returns it |
| Operation | Description |
| --- | --- |
| graph.add_node(node) | Adds a new node to the graph |
| graph.add_edge(node1, node2) | Adds an edge between two nodes |
| dfs(graph) | Performs a depth-first search on the graph |
| bfs(graph) | Performs a breadth-first search on the graph |
Algorithms
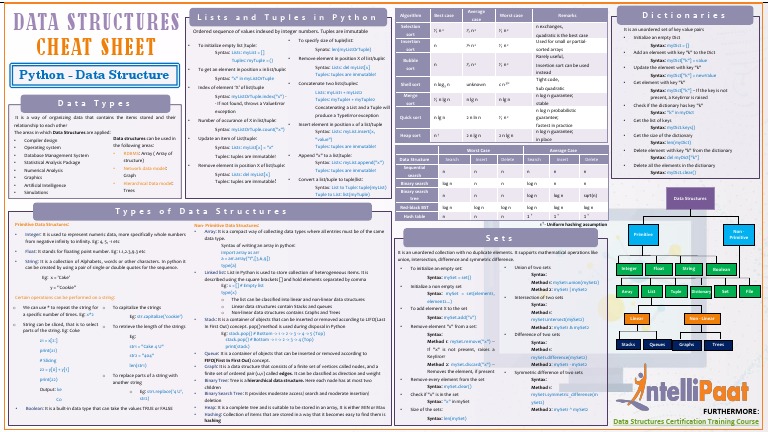
Sorting Algorithms Bubble Sort: Repeatedly compares adjacent elements and swaps them if they are in the wrong order. Insertion Sort: Builds the final sorted array by iterating through the input array and inserting each element into its proper position. Selection Sort: Selects the smallest (or largest) element from the unsorted portion of the array and moves it to the beginning (or end) of the sorted portion. Merge Sort: Divides the input array into two halves, recursively sorts each half, and then merges the two sorted halves back together. Quick Sort: Picks a pivot element, partitions the input array around the pivot, and recursively sorts the subarrays on either side of the pivot. Searching Algorithms Linear Search: Iterates through the entire array to find an element. Binary Search: Divides the input array in half repeatedly until the target element is found or it's determined that the element is not present. Graph Traversal Algorithms Depth-First Search (DFS): Visits a node, then recursively visits its neighbors before backtracking. Breadth-First Search (BFS): Visits all nodes at a given depth level before moving on to the next depth level. Dynamic Programming| Problem | Description |
| --- | --- |
| Fibonacci Sequence | Calculates the n-th Fibonacci number using memoization. |
| Longest Common Subsequence | Finds the longest contiguous subarray common to two input arrays. |
Greedy Algorithms Huffman Coding: Builds a prefix tree and encodes symbols based on their frequency. Activity Selection Problem: Selects the maximum set of activities that can be performed without conflict, given a list of start and end times for each activity.Additional Tips
Usebisect module for binary search. Utilize recursion to solve problems more efficiently. Practice sorting and searching algorithms on random input data. Study graph traversal algorithms and dynamic programming solutions. Familiarize yourself with common interview questions and practice solving them.
This cheat sheet provides a comprehensive overview of Python's most popular data structures and algorithms, along with their respective operations and descriptions. By following this guide, you'll gain a solid understanding of these fundamental concepts and be well-prepared for future programming challenges!
Sorting algorithms cheat sheet Python
I'd be happy to help you with that!
Here's a comprehensive sorting algorithm cheat sheet in Python:
1. Bubble Sort
def bubble_sort(arr):
n = len(arr)
for i in range(n-1):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
2. Selection Sort
def selection_sort(arr):
n = len(arr)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
3. Insertion Sort
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i-1
while j >= 0 and key < arr[j]:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
return arr
4. Quick Sort
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr)-1]
left_half = [x for x in arr[:-1] if x < pivot]
middle = [x for x in arr if x == pivot]
right_half = [x for x in arr[:-1] if x > pivot]
return quick_sort(left_half) + middle + quick_sort(right_half)
5. Merge Sort
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr)//2
left_half = merge_sort(arr[:mid])
right_half = merge_sort(arr[mid:])
return merge(left_half, right_half)
def merge(left, right):
result = []
while len(left) > 0 and len(right) > 0:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
result.extend(left)
result.extend(right)
return result
6. Heap Sort
import heapq
def heap_sort(arr):
return list(heapq.nlargest(len(arr), arr))
7. Radix Sort
def radix_sort(arr):
max_digit = 0
for num in arr:
if len(str(num)) > max_digit:
max_digit = len(str(num))
for digit in range(max_digit):
buckets = [[] for _ in range(10)]
for num in arr:
bucket_idx = (int(str(num)[digit]) - 1) % 10
buckets[bucket_idx].append(num)
arr = []
for bucket in buckets:
arr.extend(bucket)
return arr
8. Tim Sort
This is the default sorting algorithm used by Python, which combines elements of merge sort and insertion sort.
Note: The above code snippets are simplified examples and may not be the most efficient or robust implementations. For production use, consider using a stable sorting library like NumPy or SciPy.
I hope this helps! Let me know if you have any further questions.