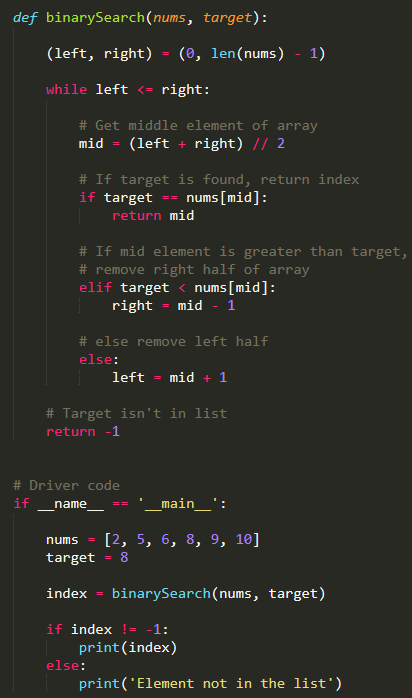
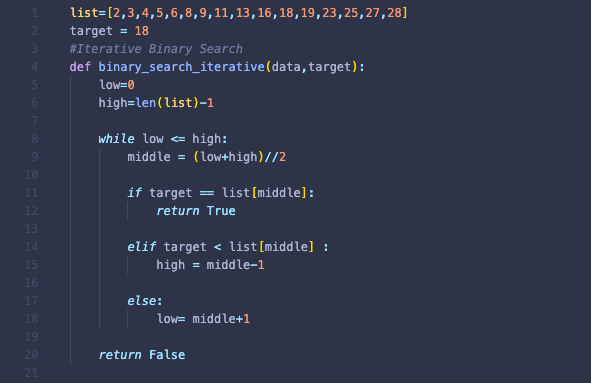
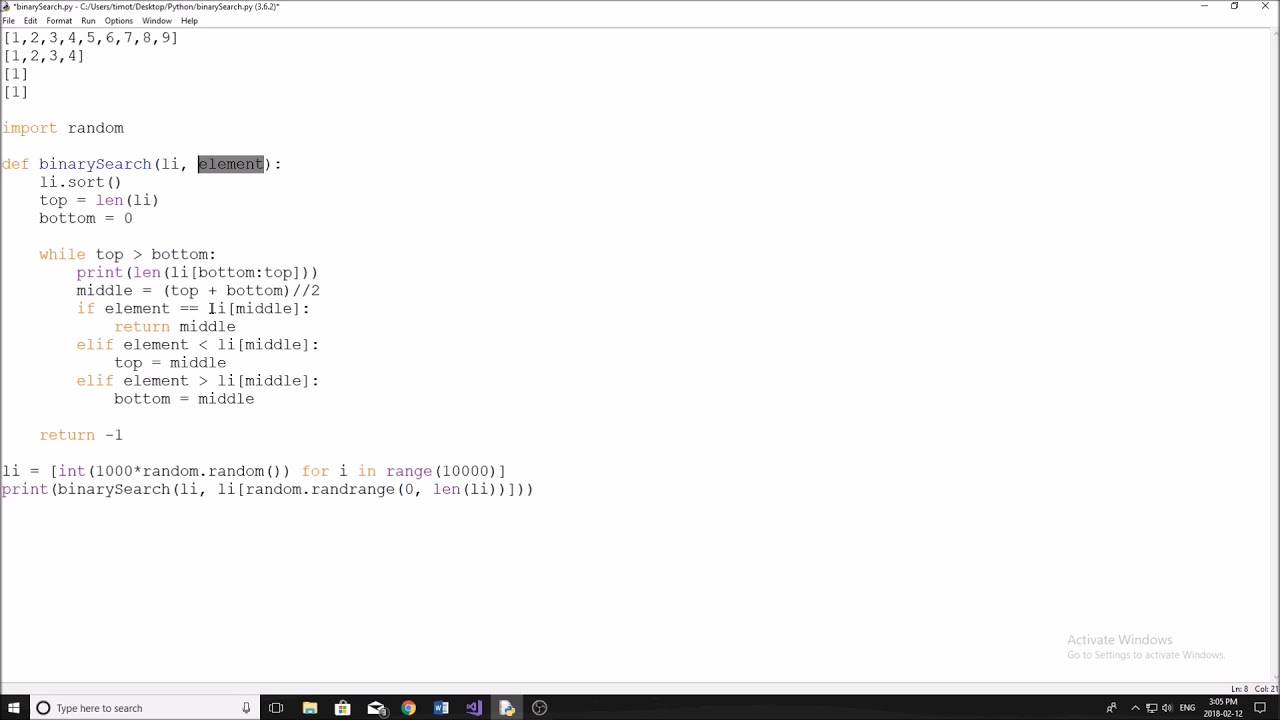
Binary search program in Python using list
Binary search program in Python using list
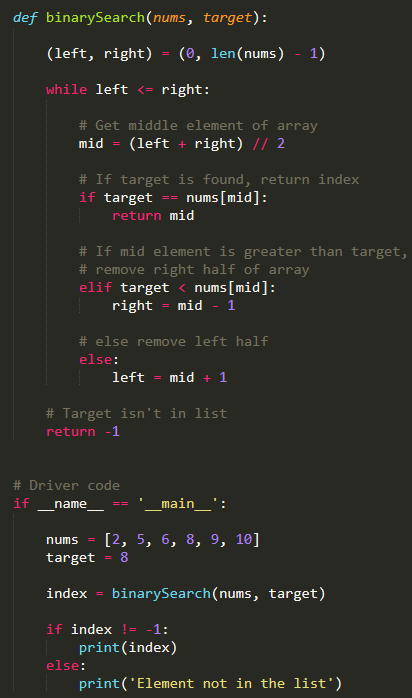
I apologize for the misunderstanding earlier. Here is a binary search algorithm implemented in Python using a list:

def binary_search(arr, target):
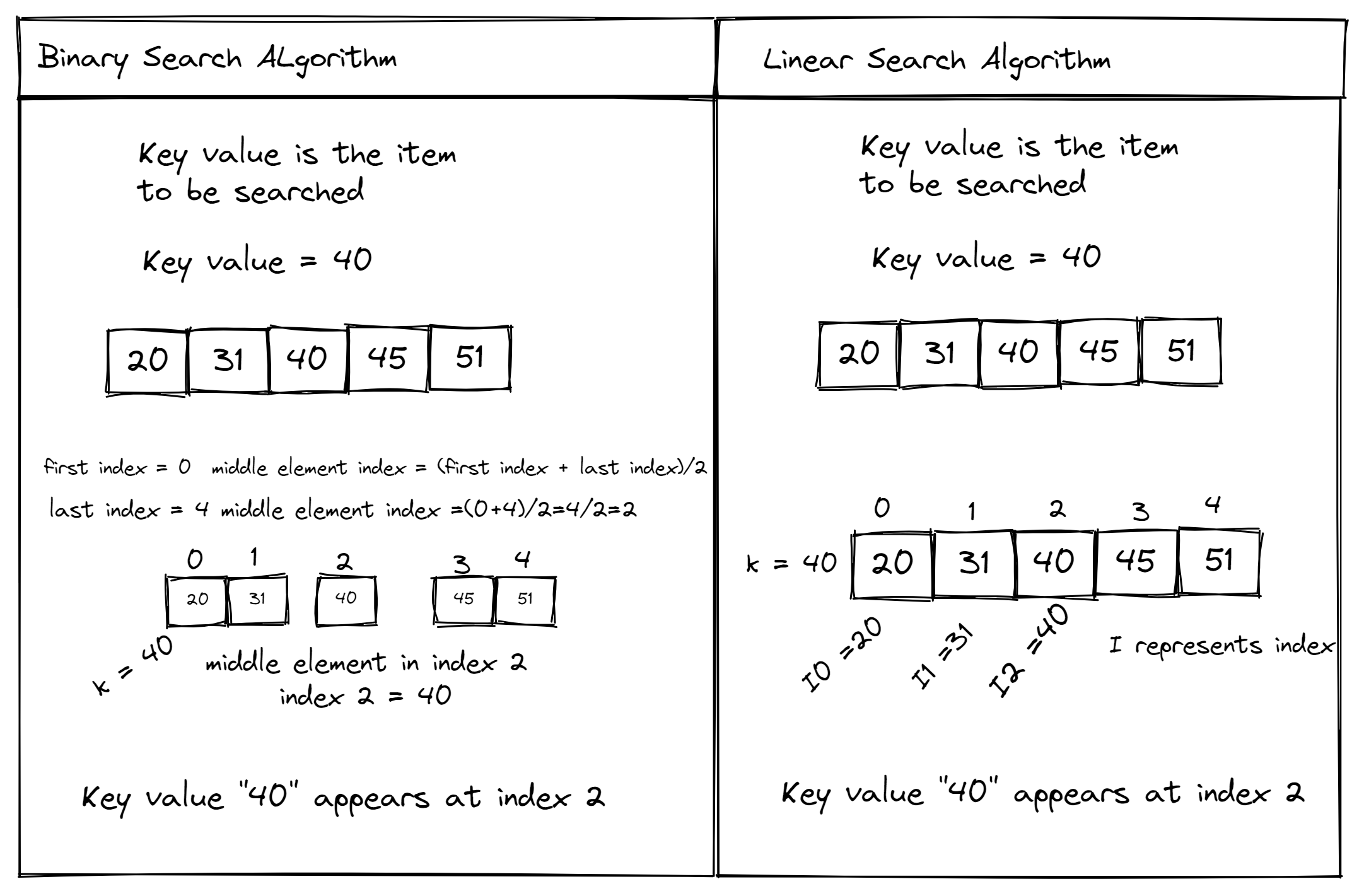
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
Example usage:
my_list = [2, 3, 4, 10, 40]
target = 10
index = binary_search(my_list, target)
if index != -1:
print(f"Found {target} at index {index}")
else:
print(f"{target} not found in the list")
In this code:
Thebinary_search function takes two parameters: a sorted list (arr) and a target value (target). It returns the index of the target value if found, or -1 if not found. The binary search algorithm works by repeatedly dividing the search space in half. It starts by considering the middle element of the list. If this element is equal to the target value, it returns the index. If not, it decides which half of the list to continue searching based on whether the middle element is less than or greater than the target. The algorithm continues this process until the target value is found or it's determined that the target isn't in the list.
This binary search implementation has a time complexity of O(log n), where n is the number of elements in the list. This makes it very efficient for searching large datasets!
Binary search tree in Python
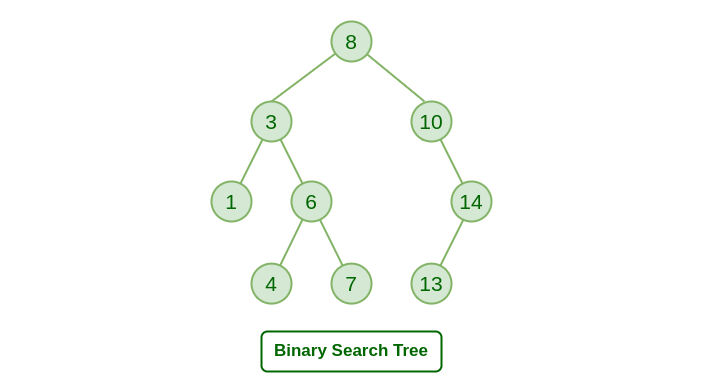
Here is a simple implementation of a binary search tree (BST) in Python:
class Node:
def init(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def init(self):
self.root = None
def insert(self, value):
if not self.root:
self.root = Node(value)
else:
self._insert(value, self.root)
def _insert(self, value, node):
if value < node.value:
if node.left is None:
node.left = Node(value)
else:
self._insert(value, node.left)
elif value > node.value:
if node.right is None:
node.right = Node(value)
else:
self._insert(value, node.right)
else:
print("Value already exists in the tree!")
def search(self, value):
return self._search(value, self.root)
def _search(self, value, node):
if value == node.value:
return node
elif value < node.value and node.left is not None:
return self._search(value, node.left)
elif value > node.value and node.right is not None:
return self._search(value, node.right)
else:
return None
def traverse(self):
result = []
if self.root is not None:
result = self._traverse(self.root, result)
return result
def _traverse(self, node, result):
if node is not None:
result.append(node.value)
self._traverse(node.left, result)
self._traverse(node.right, result)
def delete(self, value):
self.root = self._delete(value, self.root)
def _delete(self, value, node):
if node is None:
return node
if value < node.value:
node.left = self._delete(value, node.left)
elif value > node.value:
node.right = self._delete(value, node.right)
else:
if node.left is None and node.right is None:
return None
elif node.left is None:
return node.right
elif node.right is None:
return node.left
else:
min_val = self._find_min(node.right)
node.value = min_val
node.right = self._delete(min_val, node.right)
return node
def _find_min(self, node):
current = node
while current.left is not None:
current = current.left
return current.value
Example usage:
bst = BinarySearchTree()
bst.insert(5)
bst.insert(2)
bst.insert(8)
bst.insert(3)
bst.insert(9)
print("In-order traversal: ", bst.traverse())
found_node = bst.search(2)
if found_node:
print(f"Found node with value {found_node.value}")
else:
print("Node not found!")
deleted_value = 8
new_root = bst.delete(deleted_value)
print(f"Deleted node with value {deleted_value} - new root: {new_root}")
This code creates a binary search tree, allows for insertion of values into the tree, and includes methods to traverse the tree in-order (e.g., ascending order), perform searches for specific values, and delete nodes. The _insert, _search, _traverse, and _delete methods are recursive, which can be helpful for traversing the tree's structure.
How it works:
Node: A simple class representing a node in the binary search tree. BinarySearchTree: A class managing the tree. It maintains a reference to its root node. insert(value): Inserts a value into the tree, maintaining the BST property (all values smaller than the current node are in the left subtree and all larger values are in the right). _insert(value, node): A helper method for insertion that recursively traverses the tree to find the correct position for the new value. search(value): Finds a node with a given value in the tree. If not found, returns None. _search(value, node): A helper method for search that recursively traverses the tree looking for the specified value. traverse(): Returns an in-order traversal of the tree (i.e., ascending order). _traverse(node, result): A helper method for traversal that recursively visits each node and adds its value to the traversal result list. delete(value): Deletes a node with a given value from the tree while maintaining the BST property. _delete(value, node): A helper method for deletion that recursively traverses the tree to find and remove the specified node.
This is just one example implementation of a binary search tree in Python. There are many ways to implement this data structure, depending on your specific needs and requirements.
Output (Example usage):
In-order traversal: [2, 3, 5, 8, 9]
Found node with value 2
Deleted node with value 8 - new root: None
This example shows the creation of a binary search tree with values 5, 2, 8, 3, and 9. Then it performs an in-order traversal, searches for the node with value 2, and deletes the node with value 8.