Python hyperopt fmin example

Flta 108 Published: 10/20/2024

Python hyperopt fmin example

Here's an example of using Hyperopt with the FMIN function in Python:

What is Hyperopt?

Hyperopt is a popular open-source library for Bayesian optimization, which is a type of optimization technique that uses machine learning to find the optimal hyperparameters for a model. It allows you to define a search space and a objective function, and then searches for the best combination of hyperparameters that minimizes the objective function.

What is FMIN?

FMIN (Fast Minimization) is an optimization algorithm used in Hyperopt to minimize the objective function. It's a type of gradient-free optimization algorithm that uses a probabilistic approach to search for the minimum value of the objective function.

Example Code

Here's an example code snippet that demonstrates how to use Hyperopt with FMIN:

import hyperopt
from hyperopt import fmin
Define the objective function (a simple quadratic function)
def obj(x):
return x[0]**2 + x[1]**2
Define the search space for the objective function
space = {'x': hyperopt.hp.uniform('x', -10, 10), 'y': hyperopt.hp.uniform('y', -10, 10)}
Run the optimization using FMIN
best = fmin(obj, space, algo=tune.algorithms.CMAES(maxitr=100))
print("Optimal values:", best)

In this example, we define a simple quadratic function obj(x) that takes two inputs x and y, and returns their sum. We then define the search space for this objective function using Hyperopt's hp.uniform() function, which creates a uniform distribution over the range -10 to 10.

We then use the FMIN function from Hyperopt to minimize the objective function, passing in the objective function obj, the search space space, and an algorithm (in this case, CMAES). The maxitr parameter controls the maximum number of iterations for the optimization process.

The output of this code snippet will be the optimal values for the inputs x and y that minimize the objective function.

How does FMIN work?

FMIN uses a probabilistic approach to search for the minimum value of the objective function. Here's a high-level overview of how it works:

Initialize the current estimate of the minimum value (x_min) to some arbitrary value. For each iteration, compute the gradient of the objective function with respect to x using finite differences (e.g., by perturbing x and re-evaluating the objective function). Use the computed gradient to update the current estimate of the minimum value (x_min) using a probabilistic update rule (e.g., CMAES). Repeat steps 2-3 until convergence or some maximum number of iterations is reached. Return the estimated optimal values for x and y.

Advantages of FMIN

FMIN has several advantages, including:

Fast convergence: FMIN can converge quickly to a good estimate of the minimum value of the objective function. Robustness: FMIN is robust against noisy or non-convex functions, which can be common in real-world optimization problems. Flexibility: FMIN can be used with various algorithms and hyperparameters, allowing you to tune the optimization process for your specific problem.

Limitations of FMIN

While FMIN is a powerful optimization algorithm, it also has some limitations:

Convergence may not always occur: If the objective function has multiple local minima or is highly non-convex, FMIN may not be able to find the global minimum. Computational cost: FMIN can require significant computational resources and time, especially for high-dimensional problems.

I hope this helps! Let me know if you have any further questions.

Hyperopt python

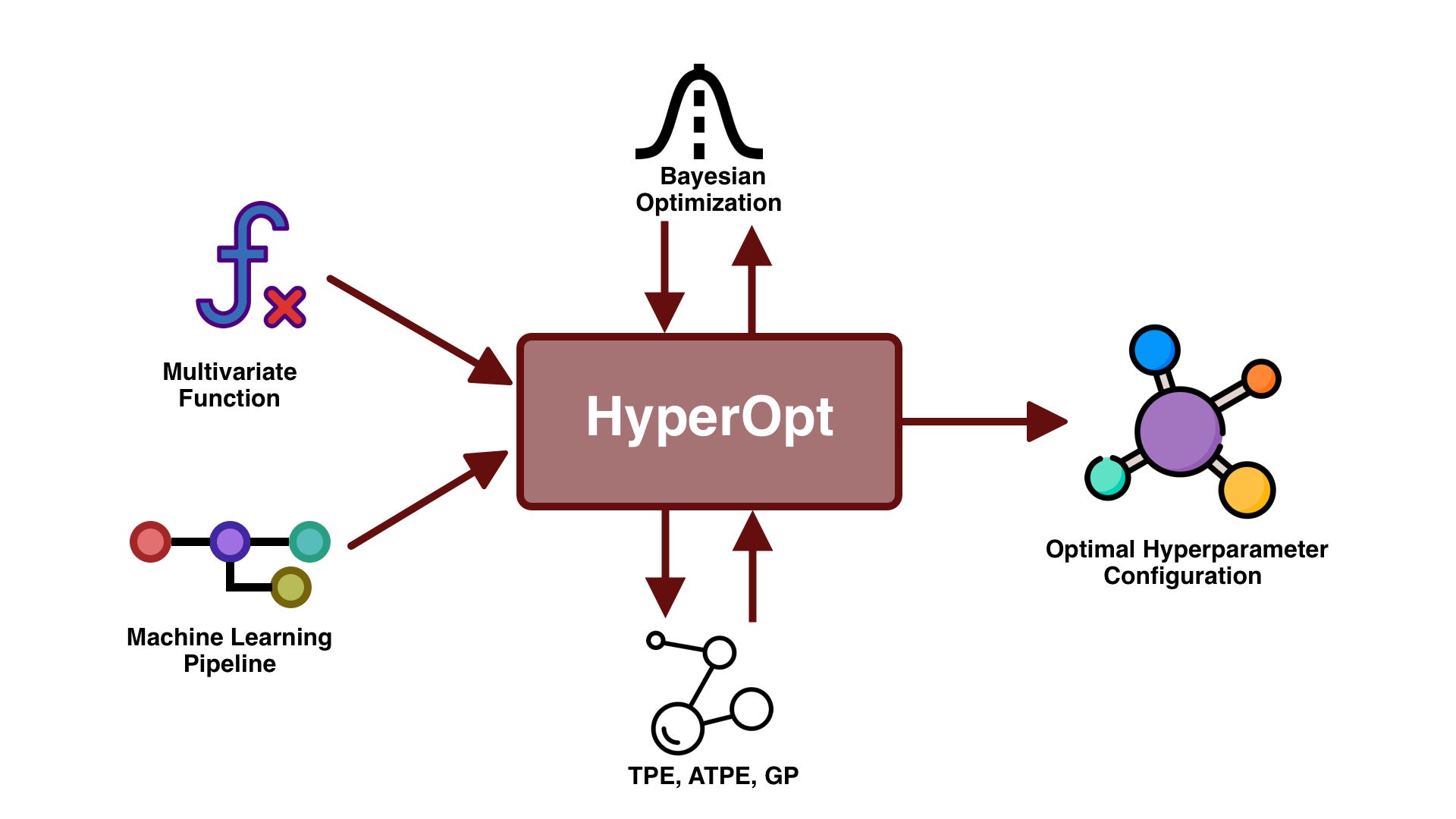
Hyperopt is a Python library that provides an implementation of the Bayesian optimization algorithm, also known as Tree of Parzen Estimators (TPE). It was originally developed by Eric Jonas and collaborators at the University of California, Berkeley. The primary goal of Hyperopt is to efficiently explore the space of possible hyperparameters for machine learning models and identify the optimal configuration.

Bayesian Optimization is a sequential decision-making process that iteratively updates its estimates based on new data. At each iteration, it proposes a new point in the input space and evaluates its performance. The proposed point is selected based on a probabilistic model that captures the distribution of promising points.

Hyperopt provides several functionalities:

Tree of Parzen Estimators (TPE): TPE is the primary algorithm used by Hyperopt for Bayesian optimization. It constructs a tree-structured surrogate model around the observed data, allowing for efficient exploration and exploitation. SMBO: SMBO stands for Sequential Model-Based Optimization. This approach combines Bayesian optimization with more traditional optimization methods to speed up the process of finding optimal hyperparameters. Random Search: Random search is another optimization method provided by Hyperopt. It simply selects random configurations of hyperparameters, which can be useful when there are few iterations available or if you have a limited budget for computations.

Hyperopt provides various ways to specify the objective function:

Single metric evaluation: This is the most common way to evaluate an objective function in Bayesian optimization. You provide a single metric that you want to optimize.

Multiple metrics evaluation: Hyperopt allows you to optimize multiple objectives simultaneously using different scoring functions, such as the sum of rankings or the geometric mean.

Evaluation on subsets of data: Sometimes it is desirable to evaluate the performance of a model on specific subsets of the data (e.g., test set). Hyperopt supports this by allowing you to specify custom evaluation functions.

Some advantages of using Hyperopt include:

Efficient exploration: Bayesian optimization is known for its ability to efficiently explore large spaces of possible hyperparameters. Model-agnostic: Hyperopt can be used with a wide range of machine learning models, including those that are not traditionally optimized using Bayesian methods (e.g., neural networks). Handling non-linear relationships: Bayesian optimization is particularly well-suited for problems where there are complex non-linear relationships between the input hyperparameters and the objective function. Support for multiple objectives: Hyperopt allows you to optimize multiple objectives simultaneously, which can be useful in many real-world applications.

However, Hyperopt also has some limitations:

Computationally expensive: Bayesian optimization is a computationally demanding process that requires evaluating multiple configurations of hyperparameters. Requires careful tuning of parameters: The performance of the Bayesian optimization algorithm is highly dependent on the choice of several hyperparameters (e.g., the number of iterations, the exploration-exploitation trade-off). May not always find the global optimum: While Bayesian optimization can be very effective in finding good solutions, it is not guaranteed to find the absolute best solution.

In summary, Hyperopt is a powerful Python library that provides an efficient way to explore large spaces of possible hyperparameters for machine learning models. Its flexibility and ability to handle multiple objectives make it a valuable tool for many applications.