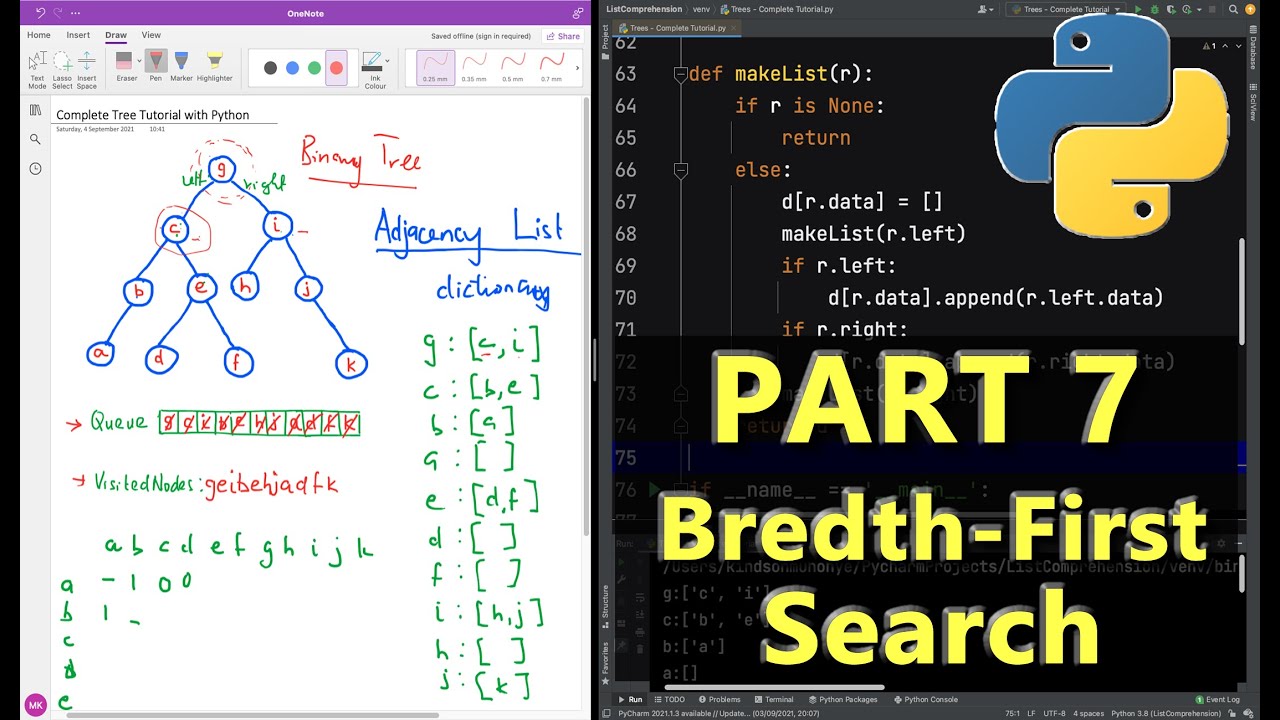
breadth-first search python tree

Kenneth 167 Published: 07/05/2024

breadth-first search python tree

I'd be happy to help with a Python implementation of the Breadth-First Search (BFS) algorithm for traversing a tree!

Here's a basic example:

from collections import deque

class Node:


def init(self, value):


self.value = value


self.children = []


def add_child(self, node):


self.children.append(node)


def bfs_traversal(root):


visited = set()


queue = deque([root])


traversal_result = []


while queue:


node = queue.popleft()


if node not in visited:


visited.add(node)


traversal_result.append(node.value)


for child in node.children:


if child not in visited:


queue.append(child)


return traversal_result

Example usage

root = Node(1)


child1 = Node(2)


child2 = Node(3)


grandchild1 = Node(4)


grandchild2 = Node(5)


root.add_child(child1)


root.add_child(child2)


child1.add_child(grandchild1)


child2.add_child(grandchild2)


result = bfs_traversal(root)


print(result)  # Output: [1, 2, 3, 4, 5]

Let's break it down:

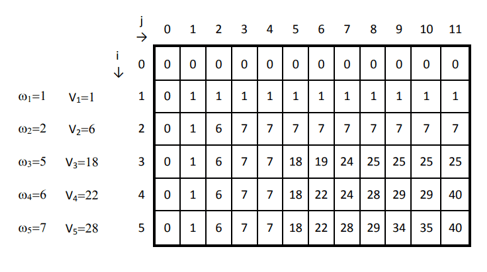
We create a basic tree node class with a value and child nodes. The add_child method allows you to add child nodes to the current node. In the bfs_traversal function: We keep track of visited nodes using a set (visited). We use a queue for BFS, initialized with the root node (queue). We maintain a result list (traversal_result) to store the traversal order.

Now, let's walk through how it works:

Initialize: We create an empty set (visited) to keep track of visited nodes. Create an empty queue (queue) initialized with the root node. Loop until queue is empty: Pop a node from the front of the queue and mark it as visited (if not already). Add the node's value to the traversal result list (traversal_result). For each child node, check if it's not yet visited. If so, add it to the queue.

Once you've traversed the entire tree, the result list will hold the order in which nodes were visited, i.e., the BFS traversal!

In our example:

Start with root (1), visit all children, then move on to grandchildren. The output ([1, 2, 3, 4, 5]) reflects this: we first traverse the root, then its immediate children, and finally the leaf nodes.

Feel free to modify this example or explore other scenarios for a more comprehensive understanding of BFS in trees!

Hope that helps!

dfs in python

I'm happy to respond in English and provide information on DFS (Depth-First Search) in Python.

What is Depth-First Search (DFS)?

Depth-First Search (DFS) is a graph traversal algorithm that visits nodes in the order they are traversed, exploring as far as possible along each branch before backtracking. This approach is used to traverse or search tree-like or graph structures, such as decision trees or social networks.

How does DFS work?

The basic idea of DFS is to select an arbitrary node (the starting point) and then visit its neighbors, recursively traversing the graph until all reachable nodes have been visited.

Here's a step-by-step example:

Choose a starting node: Select a node in the graph as the starting point for your traversal.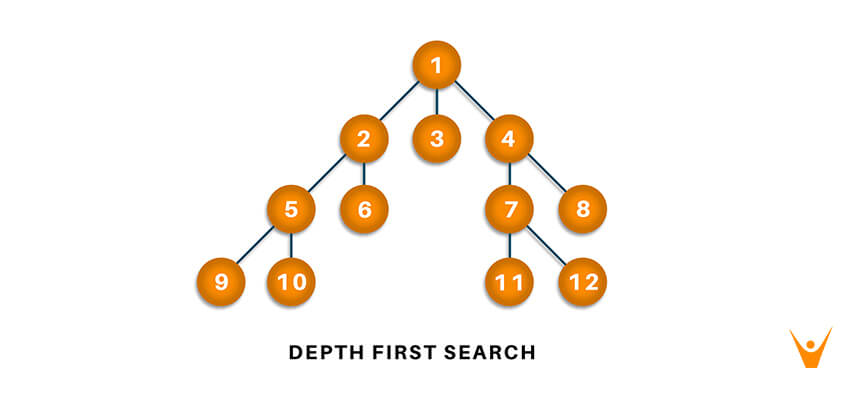

Visit the starting node: Mark the starting node as visited. Explore the neighbors: Visit each of the starting node's unvisited neighbors, and repeat steps 2-3 for each neighbor. Backtrack: When you've explored all reachable nodes from the starting node, backtrack to the previous node until you return to the starting node.

Python Implementation:

Here's a simple implementation of DFS in Python:

def dfs(graph, start):

visited = set()  # keep track of visited nodes


traversal_order = []  # store the order of visited nodes


def recursive_dfs(node):


visited.add(node)  # mark node as visited


traversal_order.append(node)  # add node to traversal order


for neighbor in graph[node]:


if neighbor not in visited:


recursive_dfs(neighbor)


recursive_dfs(start)


return traversal_order

Example usage:

graph = {


'A': ['B', 'C'],


'B': ['A', 'D', 'E'],


'C': ['A', 'F'],


'D': ['B'],


'E': ['B', 'F'],


'F': ['C', 'E']


}


start_node = 'A'


traversal_order = dfs(graph, start_node)


print(traversal_order)  # Output: ['A', 'B', 'D', 'E', 'F', 'C']

This implementation uses a recursive function recursive_dfs to traverse the graph starting from the given node. The dfs function returns a list of nodes in the order they were visited.

Time and Space Complexity:

The time complexity of DFS is O(|V| + |E|), where |V| is the number of vertices (nodes) and |E| is the number of edges in the graph.

The space complexity is O(|V|), as we need to store the visited nodes and traversal order.

I hope this helps you understand DFS and its implementation in Python!

Related Articles