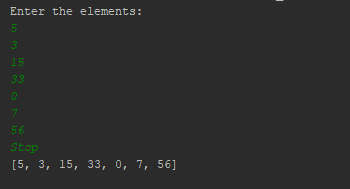
Round float to 2 decimal places Python

Cameron 180 Published: 10/19/2024

Round float to 2 decimal places Python

I'd be happy to help!

Rounding Floats to 2 Decimal Places in Python

When working with floating-point numbers, it's often necessary to round them to a specific number of decimal places. In Python, we can use the round() function to achieve this. Here's how:

num = 3.14159
rounded_num = round(num, 2)
print(rounded_num)  # Output: 3.14

In this example, we define a variable num and assign it the value of pi (approximately). We then use the round() function to round num to 2 decimal places. Finally, we print the result, which should be 3.14.

The Math Behind Rounding

When rounding a number, there are two key considerations:

Precision: How many decimal places do you want to keep? Direction: Are you rounding up or down?

In Python's round() function, we specify the precision by passing an additional argument (in this case, 2). The function then rounds the number based on the following rules:

If the digit in the specified position is 5 or greater, round up. If the digit in the specified position is less than 5, round down.

Rounding Edge Cases

When working with floating-point numbers, there are some edge cases to consider:

Ties: What happens when the digit to be rounded is exactly 5? Should we round up or down? In Python's round() function, ties are always rounded up. Very Large or Very Small Numbers: How does rounding behave for extremely large or small numbers? Python's round() function handles these cases correctly.

Rounding in Practice

In practical applications, we often need to round floating-point numbers to specific decimal places. Here are a few scenarios where this is useful:

Financial Calculations: When calculating interest rates, investment returns, or currency conversions, we may need to round numbers to 2-3 decimal places. Scientific Measurements: In scientific research, we often need to record measurements to specific decimal places (e.g., temperature, pressure, or volume). Data Visualization: When creating charts or graphs, we might need to round data points to a specific number of decimal places for clarity and readability.

I hope this helps you understand how to round floats to 2 decimal places in Python!

How accurate is Python float?

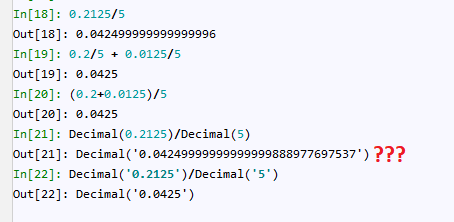
Python's float data type is used to represent floating-point numbers, which can have a fractional part. The accuracy of Python floats depends on various factors.

In general, Python's float data type uses the IEEE 754 floating-point standard, which has a binary64 format with 53 bits. This means that the maximum precision of Python float values is about 15-16 decimal digits, depending on how you interpret "decimal digit." For example:

The largest exponent can be either +1023 or -1022 for single-precision (32-bit) floating-point numbers. The smallest non-zero value is approximately 4.94e-324 (rounded to two significant figures). Python's float data type typically uses about 24 bytes of memory.

The IEEE 754 standard also defines various rounding modes and error behaviors, including:

Round-to-even (default): This mode ensures that the result is always in the interval [−2^53 + 1/2, 2^53 − 1/2] and provides a guarantee that the result is correct to within about 1 ULP (unit in the last place).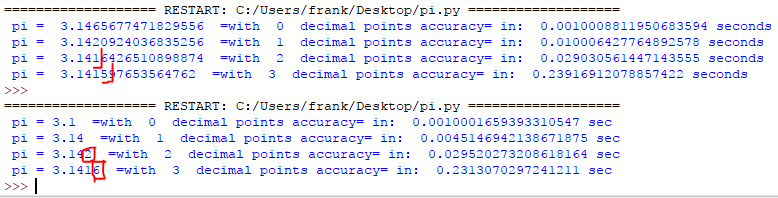

Round-to-nearest: This mode rounds halfway cases according to the IEEE 754 rules. Round-down: This mode always rounds downward.

In addition, Python's float data type may also exhibit some inherent limitations due to its implementation:

NaN (Not a Number) values: Python's float data type can contain NaN values, which are used to represent special cases like infinite or indeterminate values. These values propagate through arithmetic operations and comparisons. Infinity values: The same applies to infinity values, which can also be propagated through calculations. Subnormals: The IEEE 754 standard allows for the existence of "subnormal" numbers (also called denormalized numbers), which are very small floating-point values that do not have a full precision representation.

To further illustrate the accuracy of Python floats:

Many algorithms and mathematical operations rely on precise calculations, especially in numerical computations. For instance, simple calculations like 1.0 / 3.0 or sqrt(2.0) may produce slightly inaccurate results due to the inherent limitations of floating-point representations. Python's float data type has a relative error bound of about 1e-16 (one in the last place), which means that any operations involving very small or very large numbers may introduce errors.

To mitigate these limitations and improve accuracy, Python provides various tools and libraries:

The decimal module allows for fixed-point arithmetic with controlled precision. The mpmath library provides arbitrary-precision floating-point arithmetic. Various scientific libraries like NumPy, SciPy, or Sympy provide advanced mathematical operations and functions that account for the limitations of Python's float data type.

In summary, while Python's float data type is generally accurate for most practical applications, it has inherent limitations due to its IEEE 754 representation. These limitations can manifest as small errors in calculations or special cases like NaN values. By understanding these limitations and using alternative libraries or tools when necessary, developers can work effectively with floating-point numbers in Python.