Python operator Airflow
Python operator Airflow
I'd be happy to help you with that!
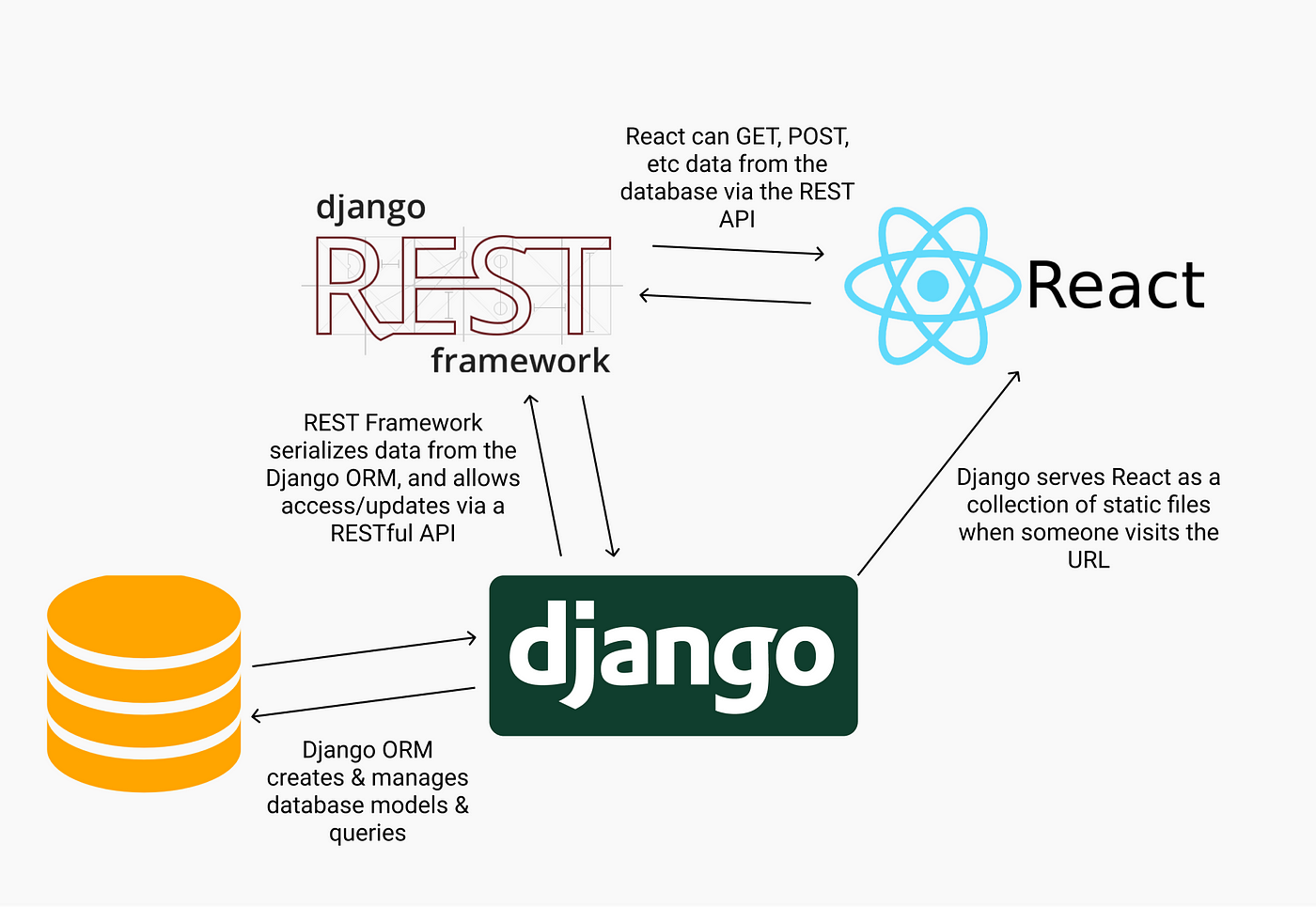
Python is a popular programming language used for data analysis, machine learning, and automation. Apache Airflow (formerly known as Luigi) is an open-source platform for programmatically defining, scheduling, and monitoring workflows.
What is Python Operator in Airflow?
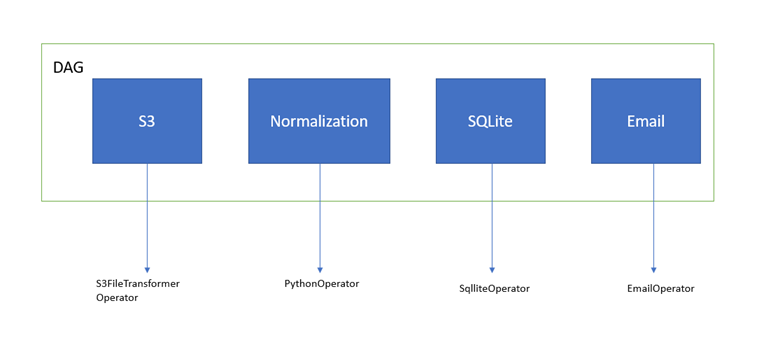
In Airflow, a Python operator is a type of task that allows you to write custom logic in Python to perform various operations within your workflow. This operator provides a way to integrate external Python code into your Airflow DAG (directed acyclic graph).
A Python operator can be used to:
subprocess module or the os library. Run external tools: Call other command-line tools or scripts, like git, make, or custom-built tools.
How to Use a Python Operator in Airflow
To use a Python operator in Airflow:
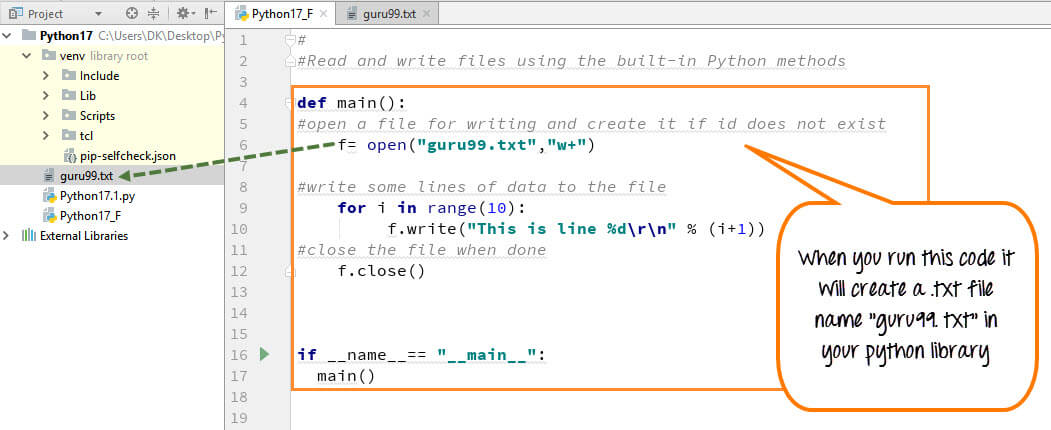
Install the required dependencies: Ensure you have the necessary Python packages installed on your system. Define the task: Create a new Python script that defines the logic for the desired operation. This file should include the necessary imports, function definitions, and execution code. Configure the operator in Airflow: In your Airflow DAG, add aPythonOperator task with the path to your Python script as an argument.
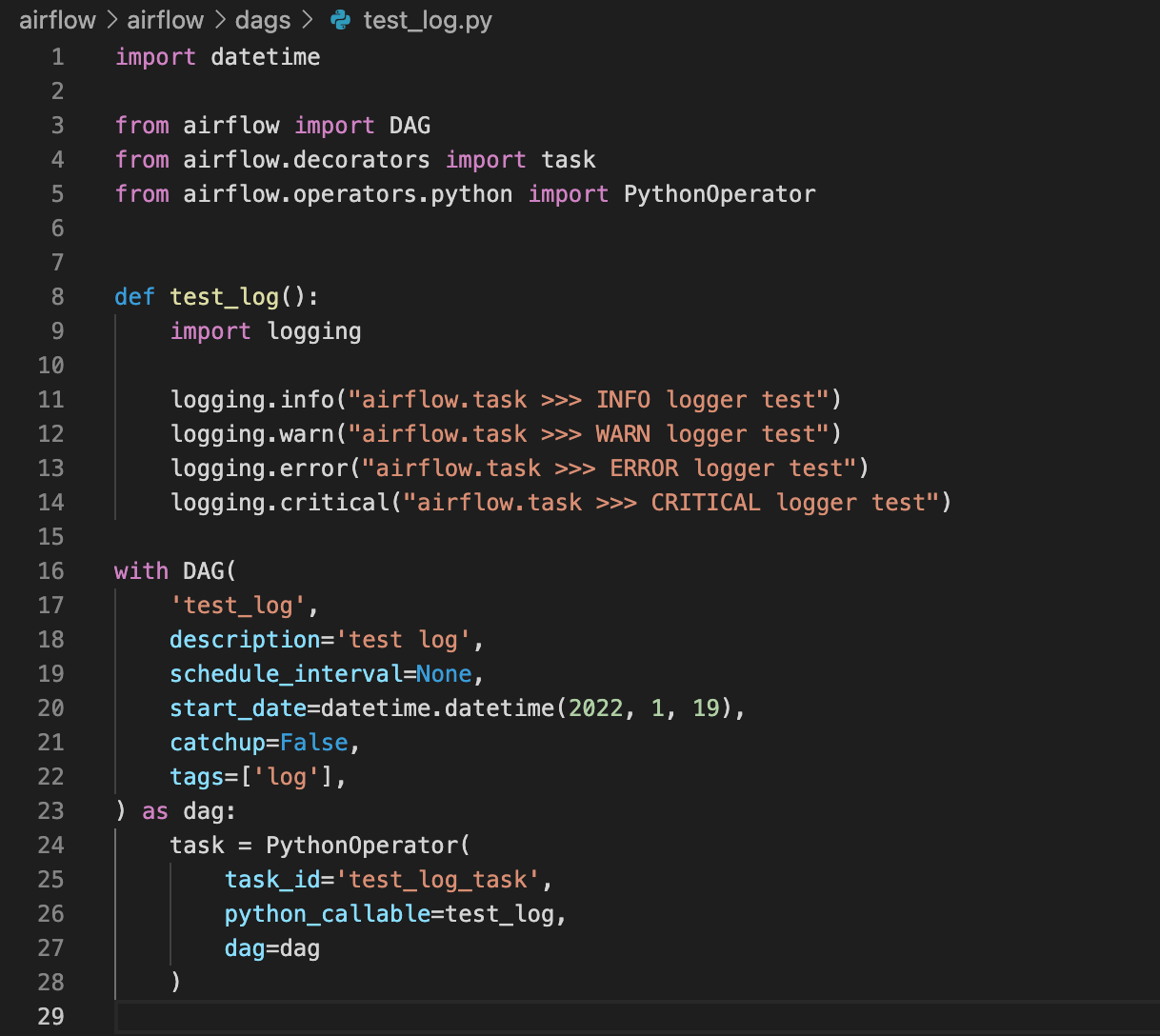
Here's a simple example:
from datetime import datetime, timedelta
from airflow.models import DAG
from airflow.operators.python_operator import PythonOperator
default_args = {
'owner': 'airflow',
'depends_on_past': False,
'start_date': datetime(2023, 3, 21),
'retries': 1,
}
dag = DAG(
'example_dag',
default_args=default_args,
schedule_interval=timedelta(days=1)
)
def my_python_function(**kwargs):
Your custom Python code hereprint("Hello from Python!")
return 'success'
t1 = PythonOperator(
task_id='my_task',
python_callable=my_python_function
)
dag.append(t1)
In this example, we define a simple Python function my_python_function and use it as the callable for a PythonOperator. When the DAG is triggered, Airflow will execute the Python script and print "Hello from Python!" to the logs.
Conclusion
The Python operator in Airflow provides an powerful way to integrate custom logic into your workflows. By leveraging Python's extensive libraries and capabilities, you can create complex tasks that interact with various systems, databases, and tools. This flexibility makes Airflow an attractive choice for a wide range of data processing and workflow automation use cases.
Do you have any specific questions or scenarios where you'd like to apply the Python operator? I'm here to help!
python @ operator numpy
A delightful topic!
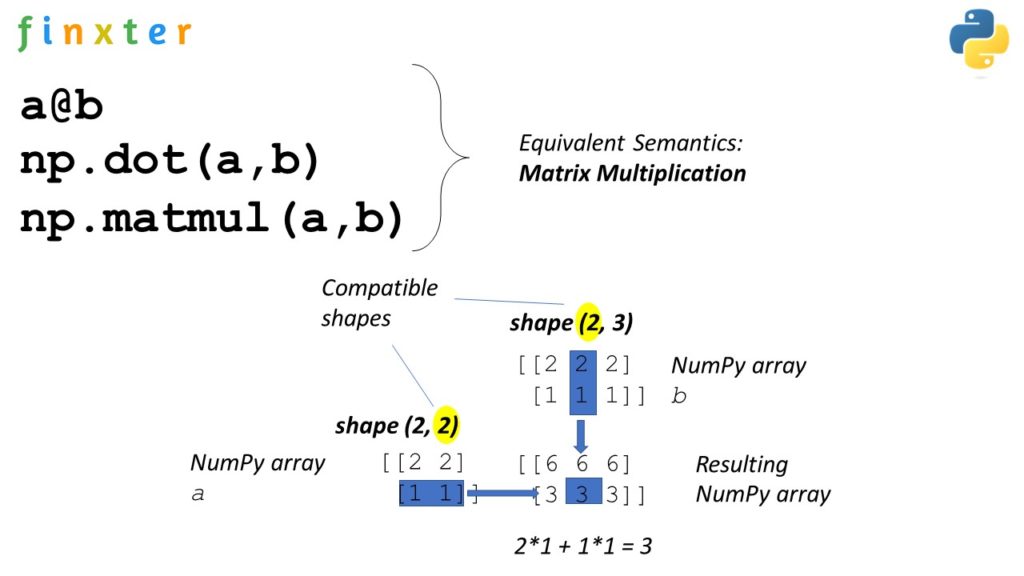
In Python, the @ symbol is called the matrix multiplication operator. It was introduced in Python 3.5 as part of the NumPy library (NumPy stands for Numerical Python).
Here's a simple example to illustrate how it works:
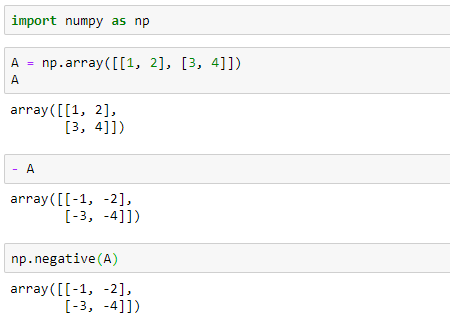
import numpy as np Create two matricesA = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
Multiply the two matrices using @ operatorC = A @ B
print(C)
In this example, A and B are 2x2 matrices. The @ operator is used to multiply them together, resulting in a new matrix C.
When you run this code, you'll see that the output is:
[[19 22],[43 50]]
So, what's happening behind the scenes?
The @ operator performs matrix multiplication according to the following rules:
Here's a more detailed explanation of how this works:
C = [[A[0][0] * B[0][0] + A[0][1] * B[1][0],A[0][0] * B[0][1] + A[0][1] * B[1][1]],
[A[1][0] * B[0][0] + A[1][1] * B[1][0],
A[1][0] * B[0][1] + A[1][1] * B[1][1]]]
In this example, the first element of C is calculated as (1*5+2*7) = 19, and so on.
This matrix multiplication operation has many applications in various fields like linear algebra, statistics, computer vision, and more. It's a fundamental concept in data processing and analysis!