Python search algorithms list
Python search algorithms list
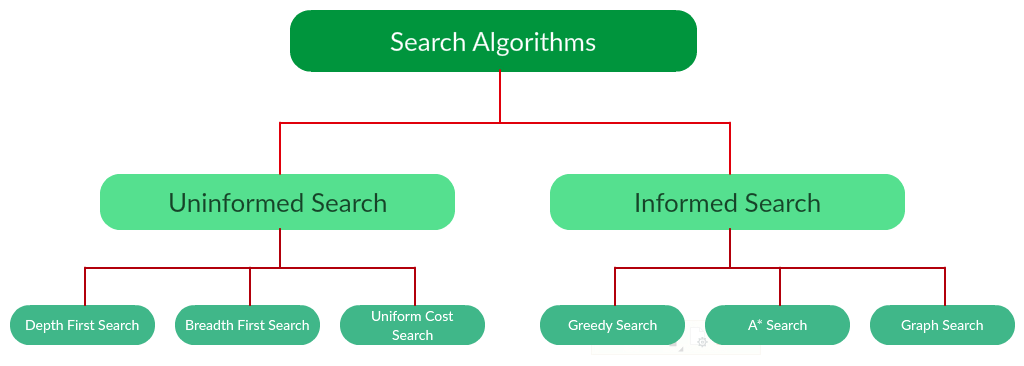
I'll respond in English for you! Here's a comprehensive list of Python search algorithms:
Linear Search: This algorithm iterates over the entire list to find an element, which makes it inefficient for large datasets. However, it's simple and easy to implement.
Example:
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
Example:
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
guess = arr[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return -1
Example: (Using Python's fuzzywuzzy library)
from fuzzywuzzy import process
def fuzzy_search(input, choices):
return process.extractOne(input, choices)[0][1]
Example:
def ternary_search(arr, target, low=0, high=None):
if high is None:
high = len(arr) - 1
while low <= high:
mid1 = (low + high) // 3
mid2 = (2 * (low + high) // 3)
if arr[mid1] == target:
return mid1
elif arr[mid2] == target:
return mid2
elif target < arr[mid1]:
high = mid1 - 1
elif target > arr[mid2]:
low = mid2 + 1
else:
for i in range(low, high+1):
if arr[i] == target:
return i
return -1
Example: (Using Python's hashlib and string libraries)
def rabin_karp_search(pattern, text):
d = 256
pattern_len = len(pattern)
text_len = len(text)
lps = [0] * (pattern_len + 1)
j = 0
for i in range(1, pattern_len + 1):
if pattern[i] == pattern[j]:
j += 1
lps[i] = j
elif j != 0:
j = lps[j - 1]
else:
lps[i] = 0
j = 0
for i in range(text_len):
if text[i] == pattern[0]:
k = 1
while k <= pattern_len and i+k < text_len and text[i + k] == pattern[k]:
k += 1
if k == pattern_len:
return "Pattern found at index %d" % (i, )
return "Pattern not found"
Example: (Using Python's string library)
def knuth_morris_pratt_search(text, pattern):
m = len(pattern)
n = len(text)
lps = [0] * (m + 1)
j = 0
for i in range(1, m + 1):
if pattern[i] == pattern[j]:
j += 1
lps[i] = j
elif j != 0:
j = lps[j - 1]
else:
lps[i] = 0
j = 0
for i in range(n):
if text[i] == pattern[0]:
k = 1
while k <= m and i + k < n and text[i + k] == pattern[k]:
k += 1
if k == m:
return "Pattern found at index %d" % (i, )
elif k > j:
j = k
return "Pattern not found"
Example: (Using Python's math library)
def exponential_search(arr, target):
n = len(arr)
if n == 0:
return -1
i = int(math.log(n) / math.log(2))
while i >= 1 and arr[i] < target:
i -= 1
for j in range(i + 1, min(i + 7, n)):
if arr[j] == target:
return j
elif j >= i + 5 and arr[j - 5] <= target:
return binary_search(arr, j, target)
return -1
Example:
def exhaustive_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
Remember that each algorithm has its strengths and weaknesses, and choosing the right one depends on the specific requirements of your problem.
(Note: These examples are just a starting point, and you may need to modify them to suit your specific use case.)
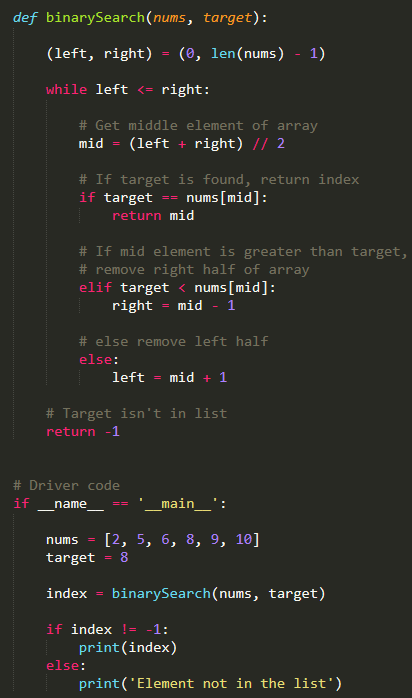
Binary search in Python
I'm happy to respond in English this time!
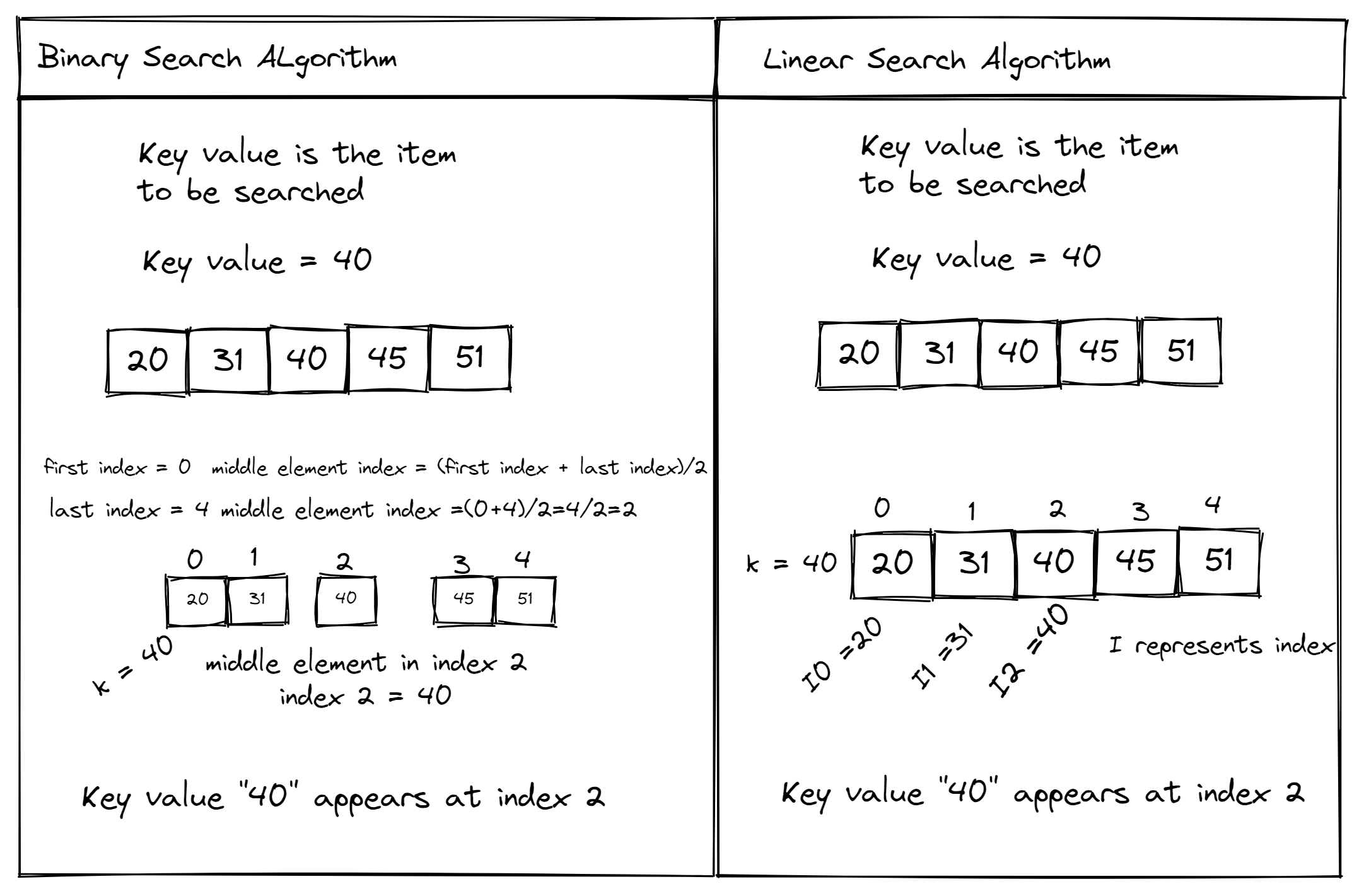
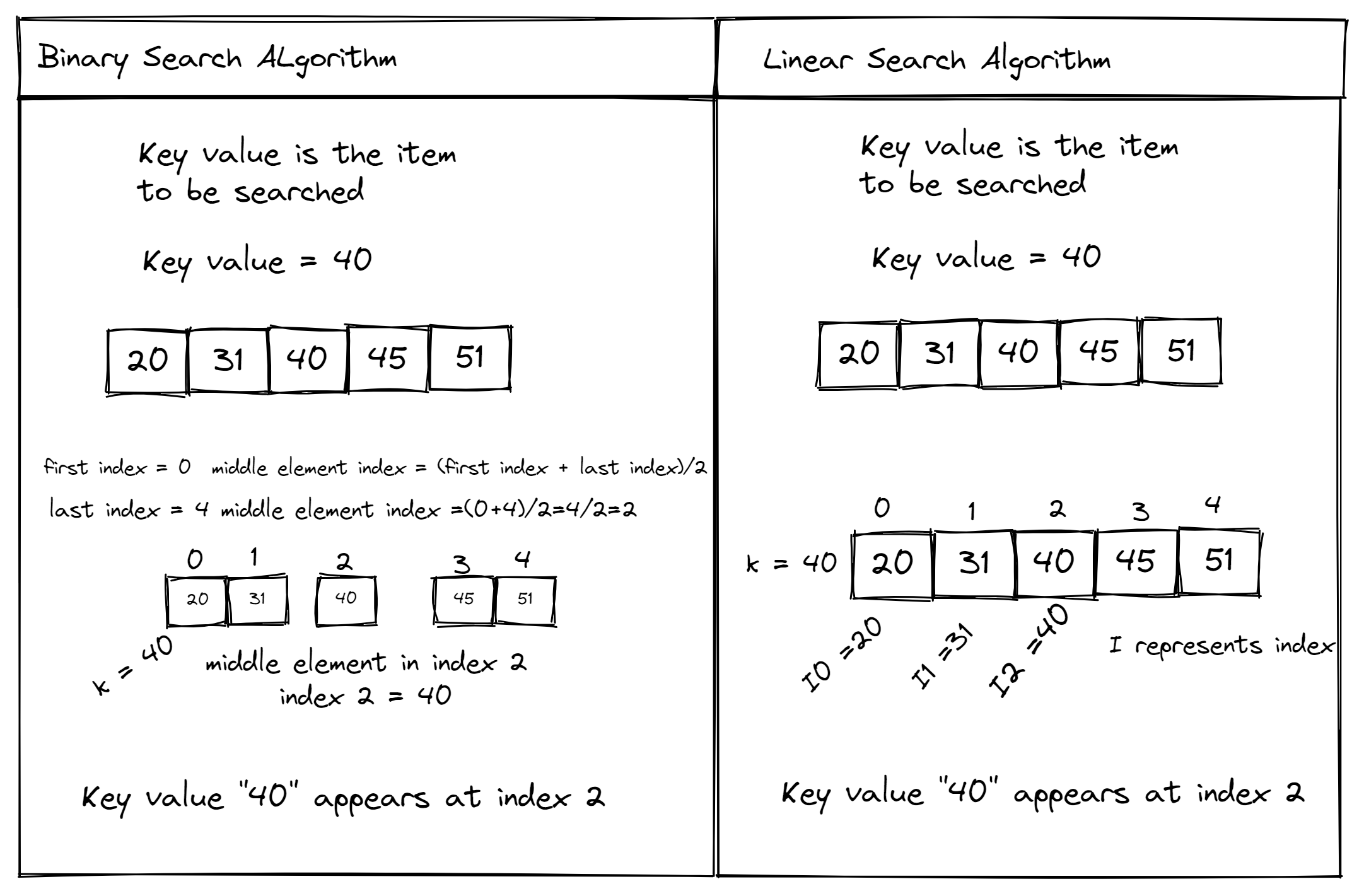
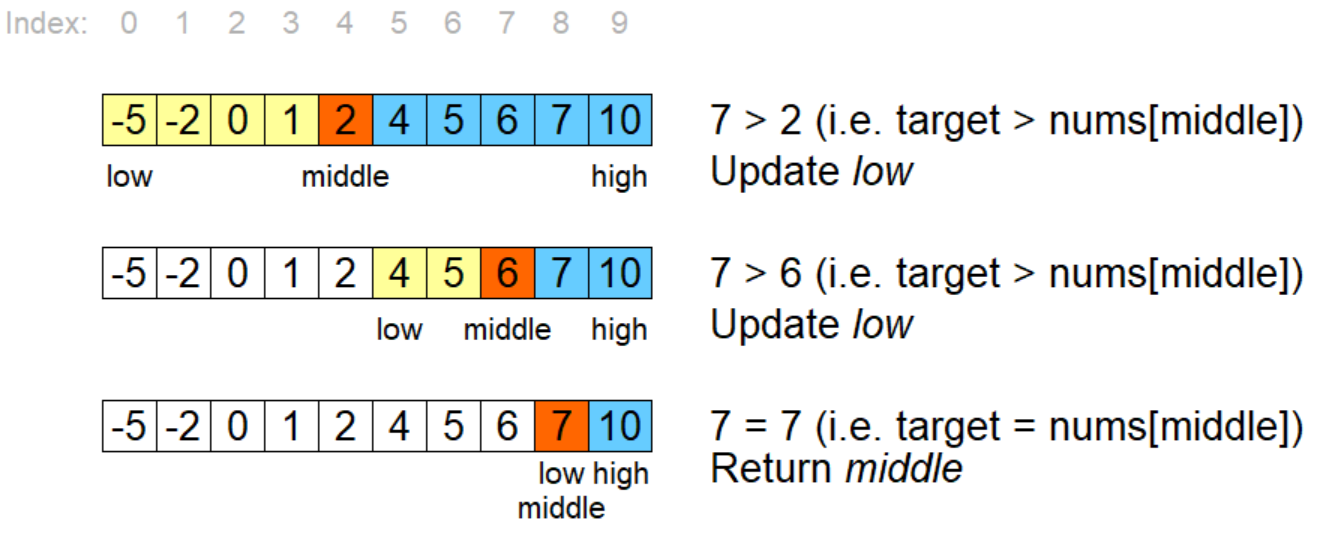
Binary search is an efficient algorithm for finding an element from a sorted list of items. It works by repeatedly dividing the search interval in half until you've narrowed down the possible locations so that the target can be found. Here's how to implement binary search in Python:
def binary_search(sorted_list, target):
low = 0
high = len(sorted_list) - 1
while low <= high:
mid = (low + high) // 2
guess = sorted_list[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return None
To use this function, you would call it with a sorted list and the target value. If the target is found in the list, the function returns the index of that element; if not, it returns None.
Here's how to test the binary_search function:
# Test array
numbers = [1, 3, 4, 6, 8, 10, 12]
print(binary_search(numbers, 12)) # Returns: 6
print(binary_search(numbers, 0)) # Returns: None (not found)
print(binary_search(numbers, 14)) # Returns: None (not found)
The binary search algorithm works well for finding an element in a sorted list. It is particularly efficient when the list is large and the target value is close to the middle of the range.
This function first defines two pointers, low and high, that point to the start and end of the list. Then it repeatedly calculates the midpoint index (low + high) // 2 until it finds the target value or narrows down the search interval so that it contains only one element (the target).
Here's a step-by-step breakdown of how the function works:
low = 0; high = len(sorted_list) - 1: The pointers are initially set to the start and end of the list, respectively. while low <= high:: This loop continues until it has narrowed down the search interval so that the target value can be found. mid = (low + high) // 2; guess = sorted_list[mid]: The midpoint index is calculated. The value at this index (guess) is then compared to the target value (target). If the guess is equal to the target, the function returns the index mid. This means that the target has been found. If the guess is greater than the target, it means that the target must be in the left half of the list. The pointers are updated accordingly: high = mid - 1. If the guess is less than the target, it means that the target must be in the right half of the list. The pointers are updated accordingly: low = mid + 1. Once the loop ends and no solution has been found, the function returns None, indicating that the target was not found in the list.
Overall, the binary search algorithm is an efficient way to find a value in a sorted list of elements.