breadth-first search python shortest path

breadth-first search python shortest path

I'd be happy to help you with that!

Breadth-First Search (BFS) Algorithm in Python

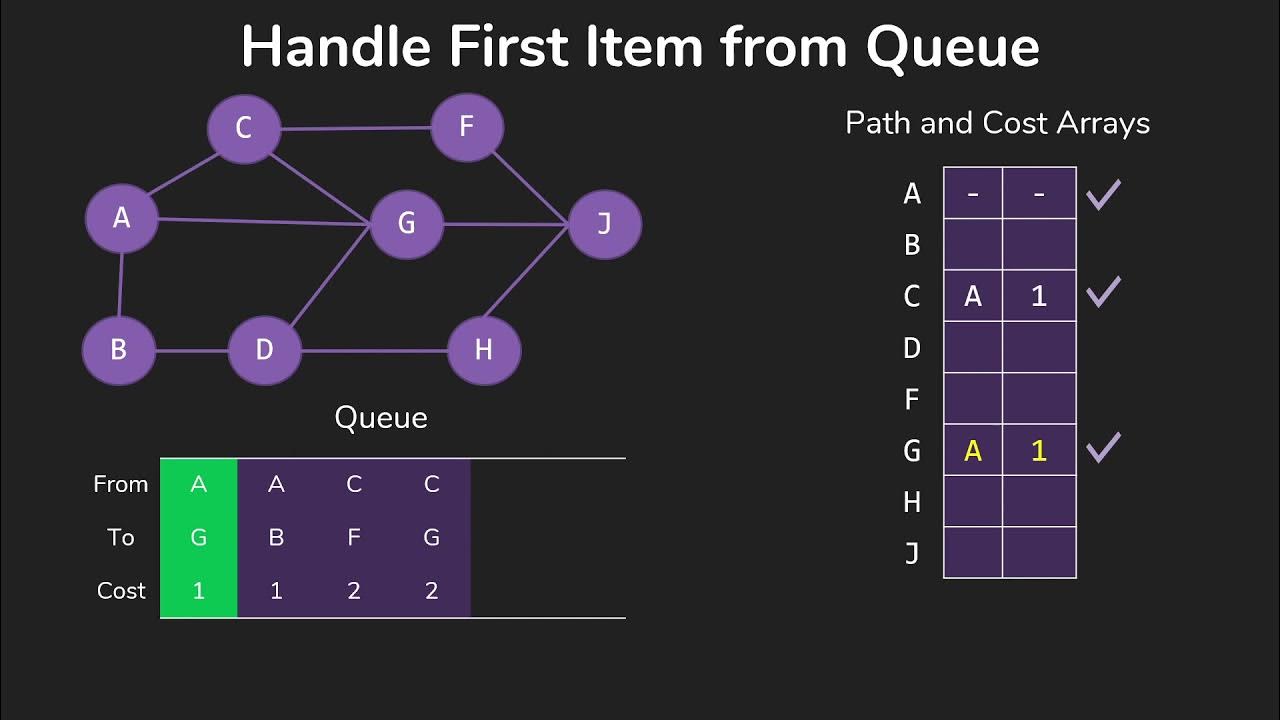
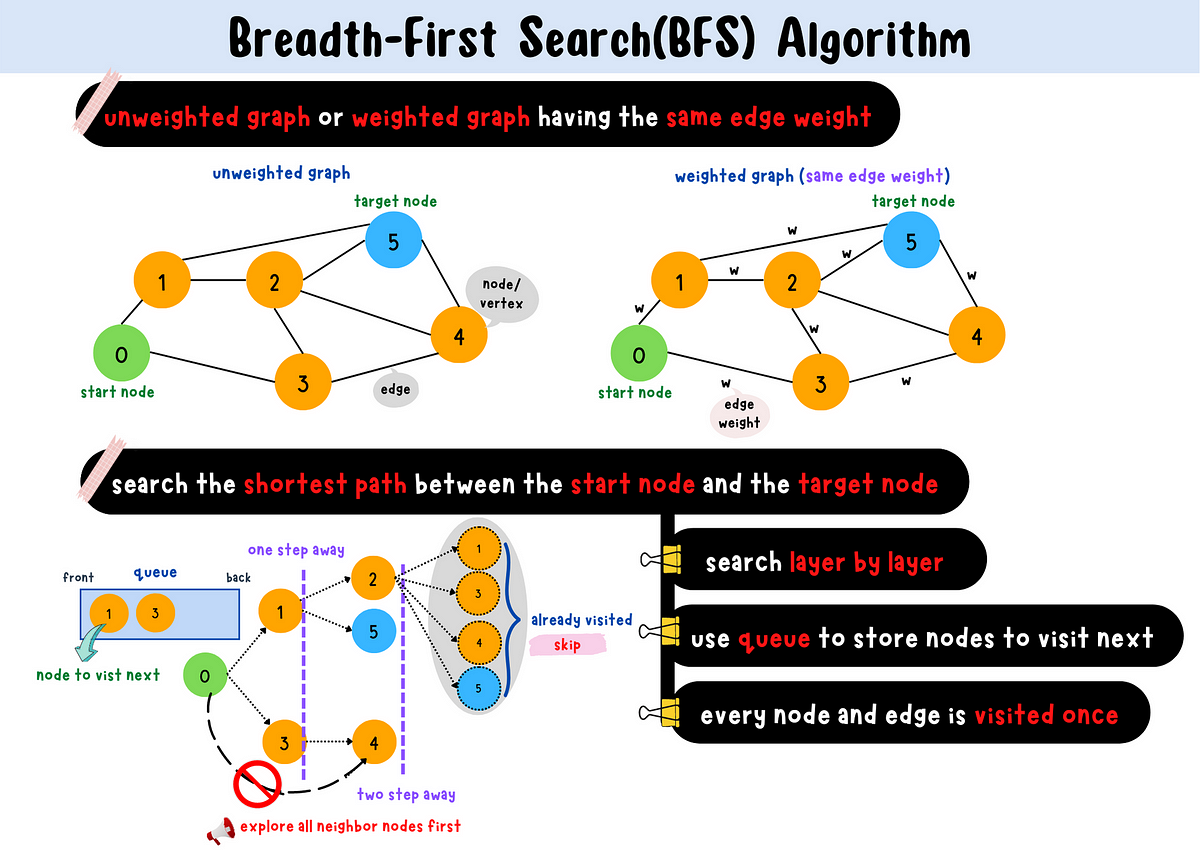
The Breadth-First Search (BFS) algorithm is a popular method for finding the shortest path between two nodes in an undirected graph or network. In this implementation, we'll use a queue data structure to keep track of the nodes to visit next.

Shortest Path Problem:

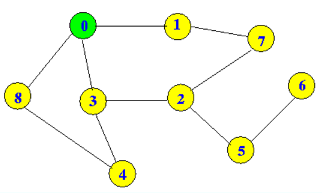
Given a weighted, connected, and undirected graph G = (V, E), where V is the set of vertices (nodes) and E is the set of edges, find the shortest path between two specified nodes s and t. The weight of each edge represents its cost or distance.

Python Implementation:

Here's the Python code to implement BFS for finding the shortest path:

from collections import deque
def bfs_shortest_path(graph, start, goal):
"""
Returns the shortest path from start to goal in the graph.
:param graph: A dictionary representing the graph, where each key is a node,
and its corresponding value is a list of adjacent nodes.
:param start: The starting node (source).
:param goal: The target node (sink).
:return: A list of nodes representing the shortest path from start to goal.
"""
Create a queue for BFS
queue = deque([[start]])  # Initialize with the starting node
while queue:
path = queue.popleft()
node = path[-1]  # Get the last node in the current path
if node == goal:  # Found the goal!
return path
for neighbor in graph.get(node, []):  # Iterate over adjacent nodes
new_path = list(path)  # Create a copy of the current path
new_path.append(neighbor)  # Add the neighboring node to the path
queue.append(new_path)
If the goal is not reachable from the start, return None
return None
Example usage:
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': ['G'],
'E': [],
'F': ['G'],
'G': []
}
start_node = 'A'
goal_node = 'G'
shortest_path = bfs_shortest_path(graph, start_node, goal_node)
print("Shortest Path:", shortest_path)  # Output: ['A', 'B', 'D', 'G']

How it Works:

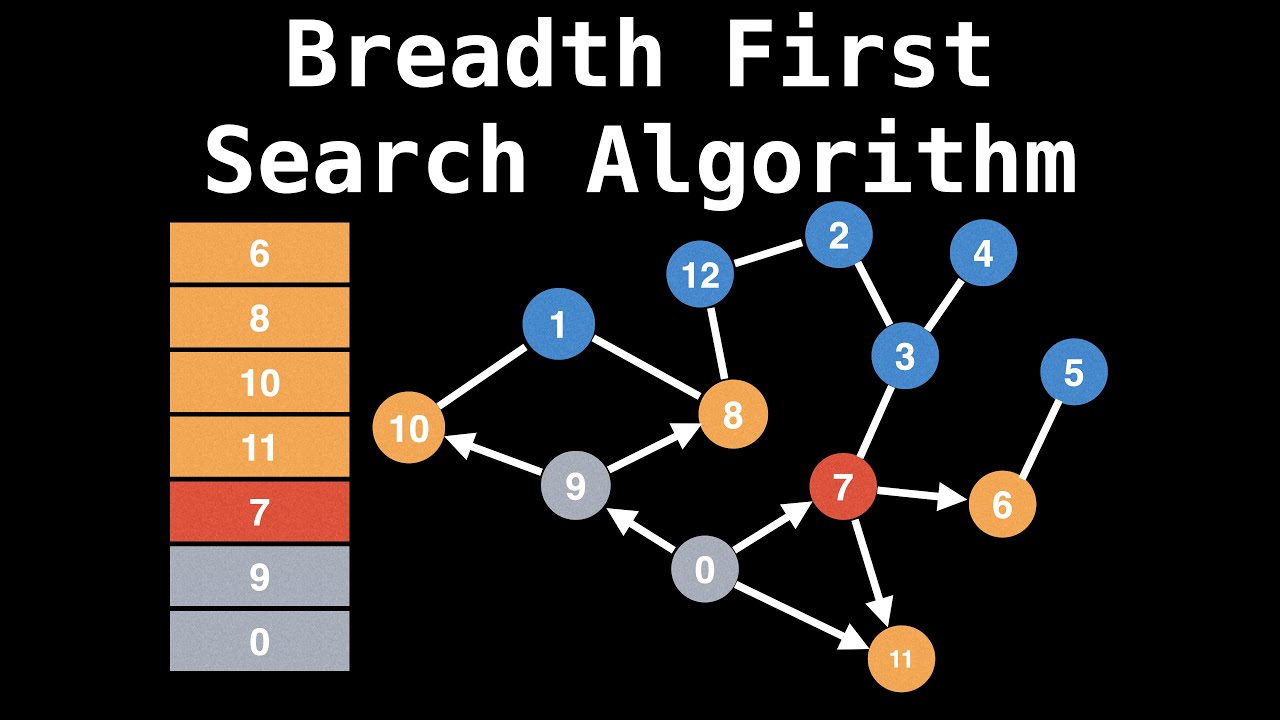
The BFS algorithm works by maintaining a queue of nodes to visit next. Initially, the queue contains only the starting node start. The algorithm then iterates through each node in the queue and for each node:

By visiting nodes level by level, BFS ensures that it explores all possible paths between the start and goal nodes before moving on to the next level. This allows it to find the shortest path efficiently.

Time Complexity:

The time complexity of BFS is O(|V| + |E|), where |V| is the number of vertices (nodes) and |E| is the number of edges in the graph. This is because we visit each node at most once, and for each edge, we perform a constant amount of work.

I hope this implementation helps you understand BFS and how to find the shortest path in an undirected graph using Python!

What is BFS and DFS in Python?

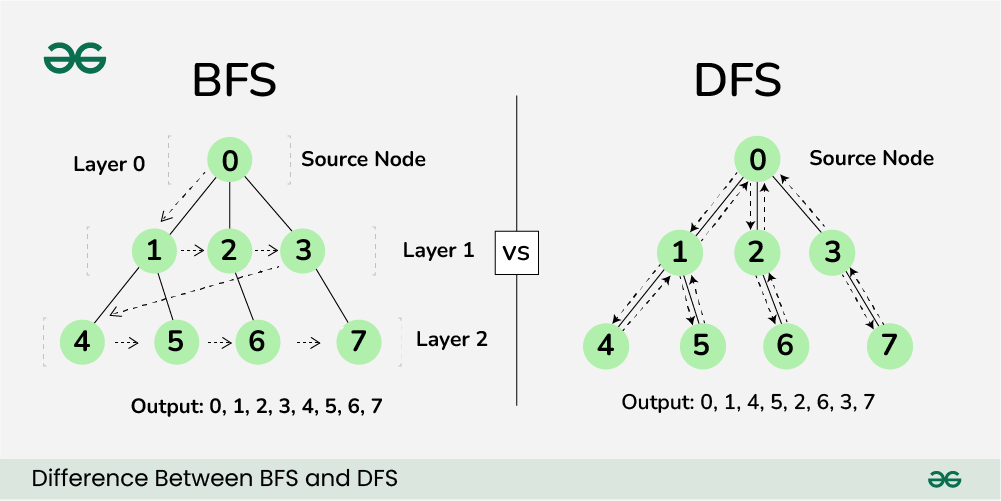
I'm happy to help! Here's the information you requested about BFS and DFS in Python:

Breadth-First Search (BFS) and Depth-First Search (DFS) are two popular algorithms used for traversing or searching through a graph or a tree data structure. In this response, I'll explain what BFS and DFS are, how they work, and provide examples of implementing them in Python.

What is BFS?

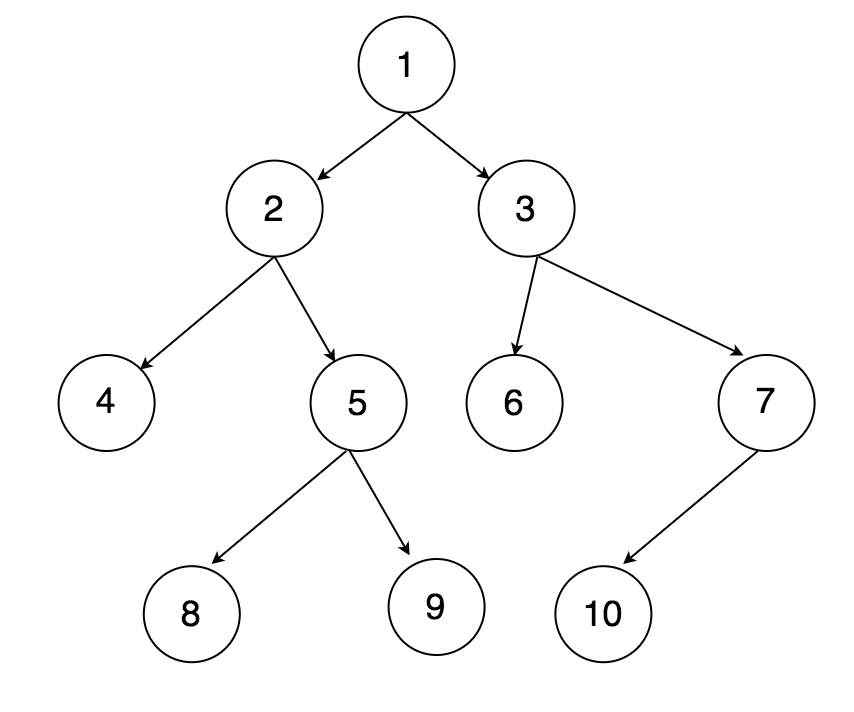
Breadth-First Search is an algorithm that explores the nodes of a graph or tree level by level, starting from a given node (also known as the "root" node). It's like traversing a maze: you move through each level until you've visited all the nodes at that level, then move on to the next level. This process continues until all nodes have been visited.

In BFS, we use a queue data structure to keep track of the nodes to visit. We start by adding the root node to the queue and mark it as visited. Then, we dequeue a node, mark it as visited, and add its unvisited neighbors to the queue. This process repeats until the queue is empty.

What is DFS?

Depth-First Search is an algorithm that explores the nodes of a graph or tree by moving as far as possible along each branch before backtracking. It's like exploring a cave: you venture deeper into the cave, and when you can't go further, you turn around and come back to where you started.

In DFS, we use recursion (a function calling itself) or an explicit stack data structure to keep track of the nodes to visit. We start by visiting the root node, then move down a branch until we reach a leaf node (a node with no children). Once we've reached a leaf node, we backtrack to the previous node and continue exploring other branches.

Example Implementations in Python

Here are some example implementations of BFS and DFS using Python:

from collections import deque
class Graph:
def init(self, vertices):
self.V = vertices
self.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]
def bfs(self, s):
visited = [False] * (self.V)
queue = deque()
visited[s] = True
print(f"Visit {s}", end=" ")
queue.append(s)
while queue:
u = queue.popleft()
for v in range(self.V):
if self.graph[u][v] == 1 and visited[v] == False:
queue.append(v)
visited[v] = True
print(f"Visit {v}", end=" ")
def dfs(self, s):
visited = [False] * (self.V)
print(f"DFS Visit {s}", end=" ")
self._dfs(s, visited)
def _dfs(self, v, visited):
visited[v] = True
print(f"Visit {v}", end=" ")
for i in range(self.V):
if self.graph[v][i] == 1 and not visited[i]:
self._dfs(i, visited)
Example usage:
g = Graph(4)
g.graph = [[1, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 1, 1],
[1, 0, 1, 0]]
print("BFS Traversal: ")
g.bfs(2)
print("nDFS Traversal: ")
g.dfs(2)

In this example, we create a simple graph with 4 vertices using an adjacency matrix representation. We then implement BFS and DFS algorithms to traverse the graph.

Conclusion

In conclusion, BFS and DFS are two fundamental algorithms used for traversing graphs or trees. While they share some similarities, they differ in their approach: BFS explores nodes level by level, whereas DFS explores as far as possible along each branch before backtracking. Understanding these algorithms is essential for any computer science student or practitioner working with graph-related problems.

I hope this response has been helpful and informative! If you have any further questions or need clarification on any of the concepts, please don't hesitate to ask.