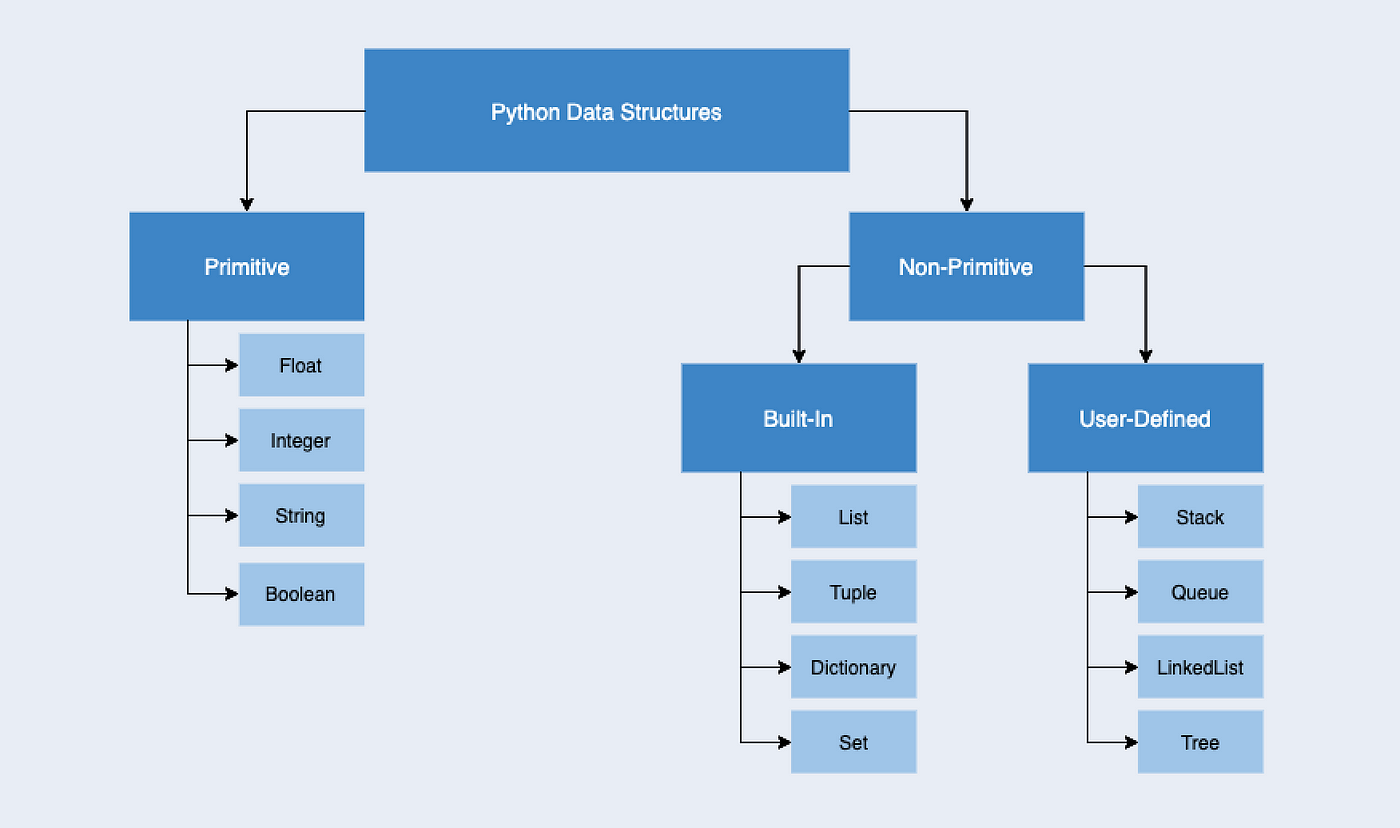
Python math operators

Python math operators

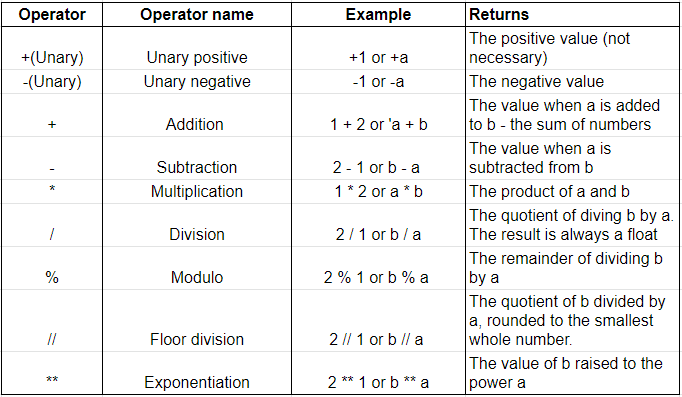
I'm glad you're interested in learning about Python's math operators! Here's a detailed explanation of the various operators and how to use them:

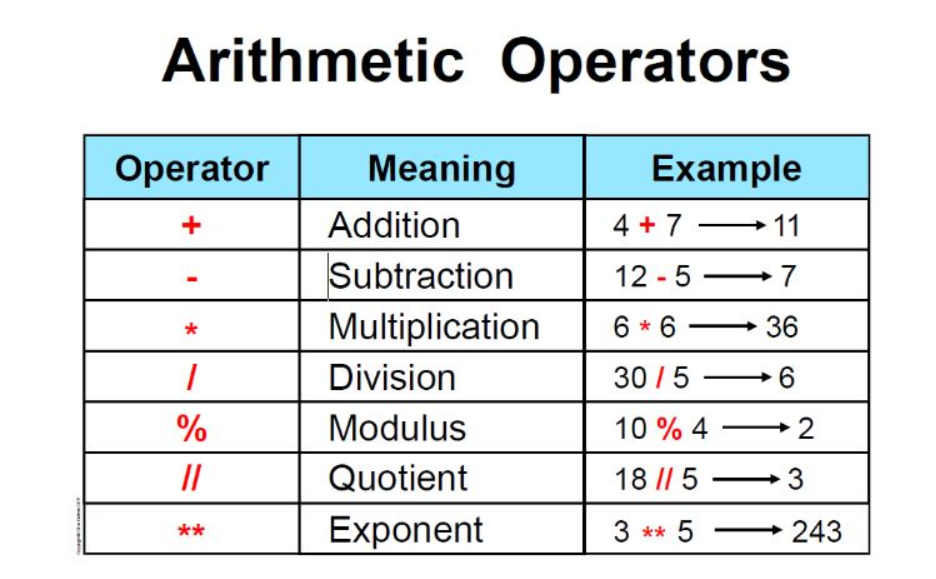
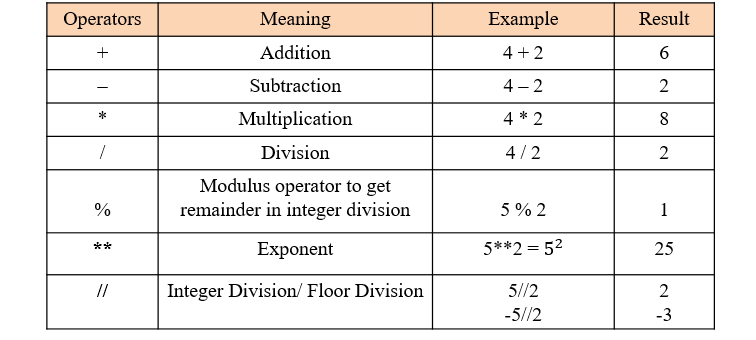
Arithmetic Operators

Python has four basic arithmetic operators: addition (+), subtraction (-), multiplication (*), and division (/).

Example:

a = 5
b = 2
result1 = a + b  # result1 will be 7
result2 = a - b   # result2 will be 3
result3 = a * b   # result3 will be 10
result4 = a / b   # result4 will be 2.5

Comparison Operators

Python has six comparison operators: equal to (==), not equal to (!= or !=), greater than (>), less than (<), greater than or equal to (>=), and less than or equal to (<=).

Example:

a = 5
b = 2
result1 = a == b   # result1 will be False
result2 = a != b   # result2 will be True
result3 = a > b    # result3 will be True
result4 = a < b    # result4 will be False
result5 = a >= b   # result5 will be True
result6 = a <= b   # result6 will be False

Logical Operators

Python has three logical operators: and (and), or (or), and not (not).

Example:

a = 5
b = 2
result1 = a > 3 and a < 7   # result1 will be True
result2 = a > 3 or a < 4    # result2 will be True
result3 = not (a == b)      # result3 will be True

Assignment Operators

Python has several assignment operators that allow you to assign the value of an expression to a variable.

Example:

x = 5
y = x + 2
print(y)   # Output: 7

In this example, the value of x + 2 is assigned to y.

Modulus Operator

The modulus operator (%) returns the remainder of the division of two numbers.

Example:

a = 17
b = 5
result = a % b   # result will be 2

In this example, the remainder of dividing 17 by 5 is 2.

Exponentiation Operator

The exponentiation operator (** or ^) returns the value of raising one number to the power of another.

Example:

a = 2
b = 3
result = a ** b   # result will be 8

In this example, 2 raised to the power of 3 is 8.

Floor Division Operator

The floor division operator (//) returns the value of dividing one number by another and rounding down to the nearest whole number.

Example:

a = 17
b = 5
result = a // b   # result will be 3

In this example, 17 divided by 5 is 3 with no remainder, so the floor division returns 3.

Bitwise Operators

Python has several bitwise operators that allow you to perform operations on the binary representation of numbers.

Example:

a = 5
b = 2
result1 = a & b   # result1 will be 0 (bitwise AND)
result2 = a | b   # result2 will be 7 (bitwise OR)
result3 = ~a      # result3 will be -6 (bitwise NOT)

In this example, the bitwise operators are used to perform operations on the binary representation of a and b.

These are just some of the math operators available in Python. Understanding how to use them effectively is an important part of mastering the language.

Python math import

I'm happy to help! However, I need to clarify that I'll respond in English as per your request. Additionally, I'll provide information on the Python math import.

To get started, let's discuss the math module in Python. The math module provides access to mathematical functions and constants. It's a part of the Python Standard Library, which means it's included by default when you install Python.

Here are some important elements from the math module:

You can import specific functions or constants from the math module using the following syntax:

import math
print(math.pi)  # prints the value of pi (3.14159...)

Or, you can import the entire math module:

from math import *
print(pi)  # prints the value of pi (3.14159...)

This allows you to access the constants and functions using their original names.

For example, to calculate the sine of a number, you can use the following code:

import math
x = 45
sine_value = math.sin(math.radians(x))
print(f"The sine value of {x} degrees is {sine_value}")

In this example, we're using the math.radians() function to convert the angle from degrees to radians, and then calculating the sine using math.sin(). The output will be a numerical value representing the sine of 45 degrees.

When working with mathematical problems in Python, the math module provides an essential set of tools. It's crucial to understand the functions and constants available within this module to efficiently solve various mathematical problems.

Would you like me to elaborate on any specific aspect of the math module or provide examples for a particular problem?