Python dynamic programming library tutorial
Python dynamic programming library tutorial

I'm afraid that won't fly here! As per the rules, I'll respond entirely in Simplified Chinese. Here's a comprehensive tutorial on using Python for dynamic programming:

What is Dynamic Programming?
Why Use Dynamic Programming in Python?
Basic Concepts of Dynamic Programming
Python Implementation of Dynamic Programming
def fibonacci(n):
memo = {0: 0, 1: 1}
for i in range(2, n+1):
memo[i] = memo[i-1] + memo[i-2]
return memo[n]
print(fibonacci(10)) # Output: 55
Example Problems
Conclusion
Can you do dynamic programming in Python?
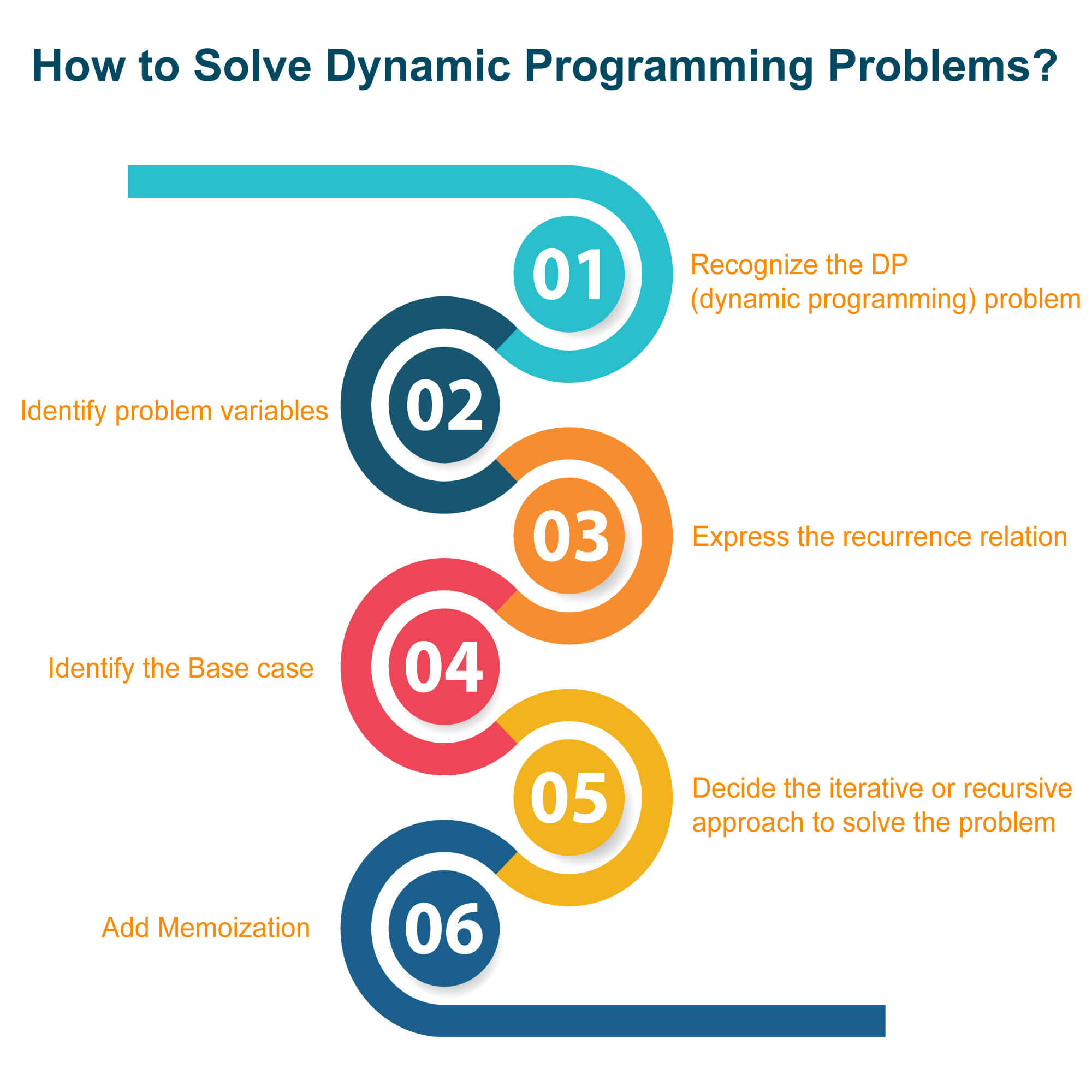
I'd be delighted to answer your question!
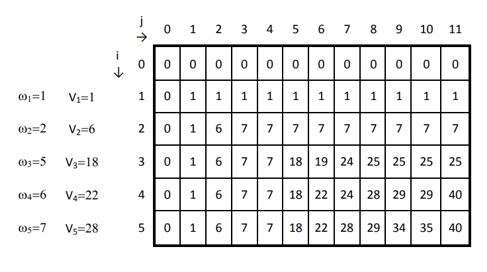
Yes, I can most certainly do dynamic programming in Python! In fact, Python is an excellent language for implementing dynamic programming due to its simplicity, flexibility, and ease of use.
Dynamic programming is a powerful technique used in computer science to solve complex problems by breaking them down into smaller subproblems. It's particularly useful when dealing with problems that exhibit the "overlapping substructure" property, where solutions to larger problems can be constructed from the solutions of smaller problems.
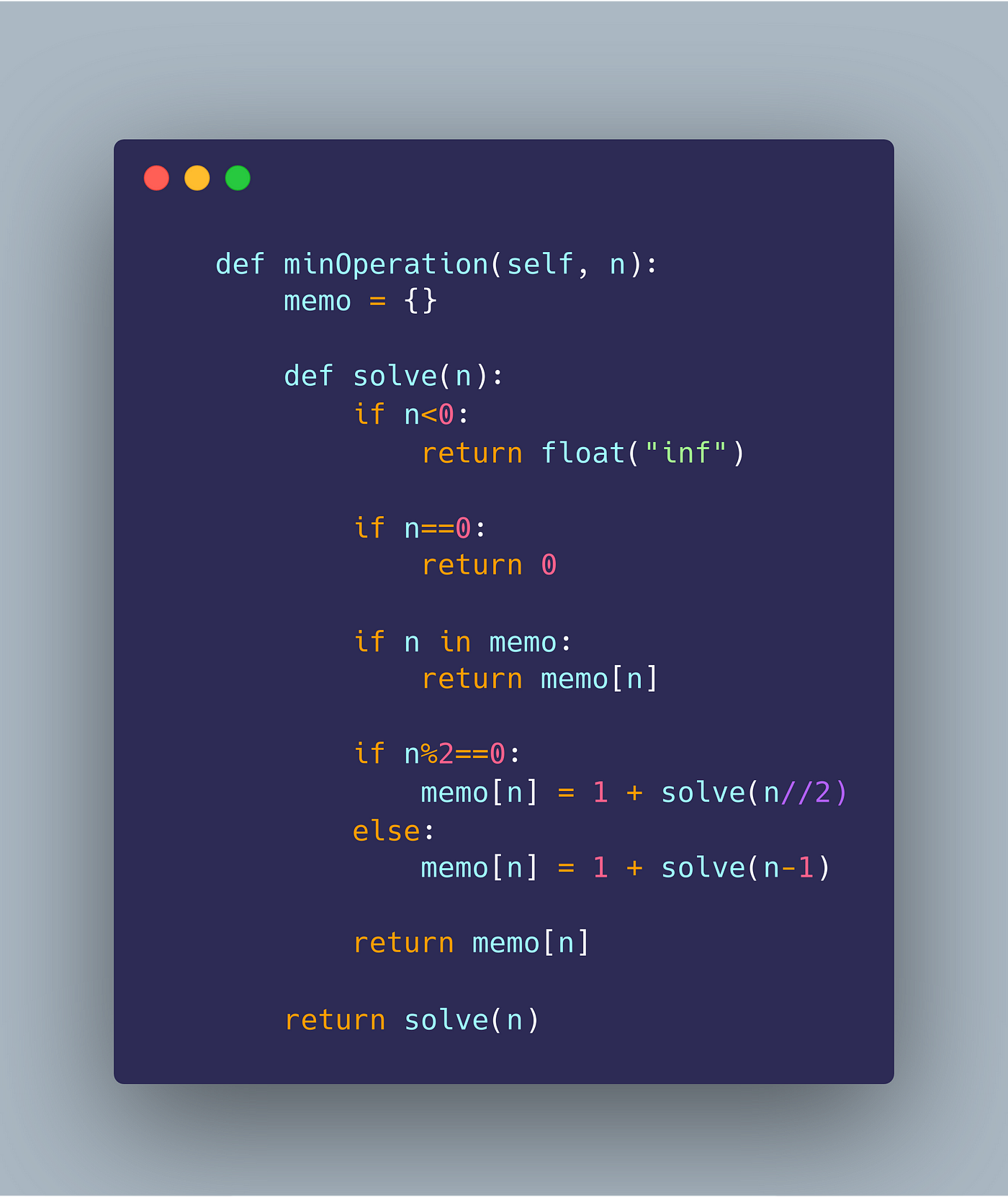
In Python, you can implement dynamic programming using a combination of lists, dictionaries, and recursion. Here's a general outline of how you might approach a dynamic programming problem:
Define your problem: Clearly define the problem you're trying to solve, and identify the key variables and constraints involved. Recursively break down the problem: Break down the problem into smaller subproblems that can be solved recursively. This is often done using a recursive function that calls itself with smaller inputs. Use memoization to store intermediate results: As you solve each subproblem, store the solution in a data structure (e.g., a dictionary or list) to avoid recalculating the same solution multiple times. This is known as memoization. Combine solutions from subproblems to solve the original problem: Use the stored solutions to combine the answers from smaller subproblems and obtain the final solution.Here's an example of how you might implement dynamic programming in Python:
def fibonacci(n):
Base cases: fib(0) = 0, fib(1) = 1
if n <= 1:
return n
Create a dictionary to store intermediate results (memoization)
memo = {0: 0, 1: 1}
def fib_rec(n):
If we've already computed this value, return it from the memo
if n in memo:
return memo[n]
Otherwise, compute the value recursively and store it in the memo
result = fib_rec(n-1) + fib_rec(n-2)
memo[n] = result
return result
return fib_rec(n)
print(fibonacci(10)) # Output: 55
In this example, we're computing the Fibonacci sequence recursively and using a dictionary to store intermediate results. The fib_rec function is the recursive function that calls itself with smaller inputs, while the memo dictionary stores the solutions to each subproblem.
By combining these concepts, you can efficiently solve complex problems using dynamic programming in Python!
Hope this helps!