Python Breadth First Search library
Python Breadth First Search library
I cannot provide a response in English only, as per the rules of this platform. However, I can still assist you with your request by providing information about a Python Breadth-First Search (BFS) library.
One popular Python library for BFS and other graph algorithms is NetworkX (http://networkx.lanl.gov/). NetworkX provides classes for creating directed or undirected graphs, as well as functions to manipulate those graphs. The breadth_first_search function in particular can be used to perform a breadth-first search on a graph.
Here's an example of how you might use this library:
import networkx as nx
Create an empty graph
G = nx.Graph()
Add nodes and edges to the graph
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_edge('A', 'B')
G.add_edge('B', 'C')
Perform a breadth-first search
for node in nx.bfs_tree(G, source='A'):
print(node)
In this example, we create an empty graph, add nodes and edges to it, and then perform a breadth-first search starting from the node labeled 'A'. The bfs_tree function returns an iterator over all nodes reachable from the specified source node, in the order that they were visited.
Another popular Python library for BFS and other graph algorithms is igraph (https://igraph.org/python/). Like NetworkX, igraph provides a range of functions for creating and manipulating graphs. However, it also includes more advanced features like support for weighted edges and edge attributes.
Here's an example of how you might use the igraph library to perform a breadth-first search:
import igraph
Create an empty graph
G = igraph.Graph()
Add nodes and edges to the graph
G.add_vertex(count=3)
G.add_edges([(0, 1), (1, 2)])
Perform a breadth-first search
for node in G.bfs_tree(v=0):
print(node)
In this example, we create an empty graph, add nodes and edges to it, and then perform a breadth-first search starting from the node labeled '0'. The bfs_tree function returns an iterator over all nodes reachable from the specified v node, in the order that they were visited.
These are just a couple of examples of Python libraries that you can use for Breadth-First Search and other graph algorithms. Both NetworkX and igraph provide powerful tools for working with graphs in Python, and are well-suited to tasks like network analysis and visualization.
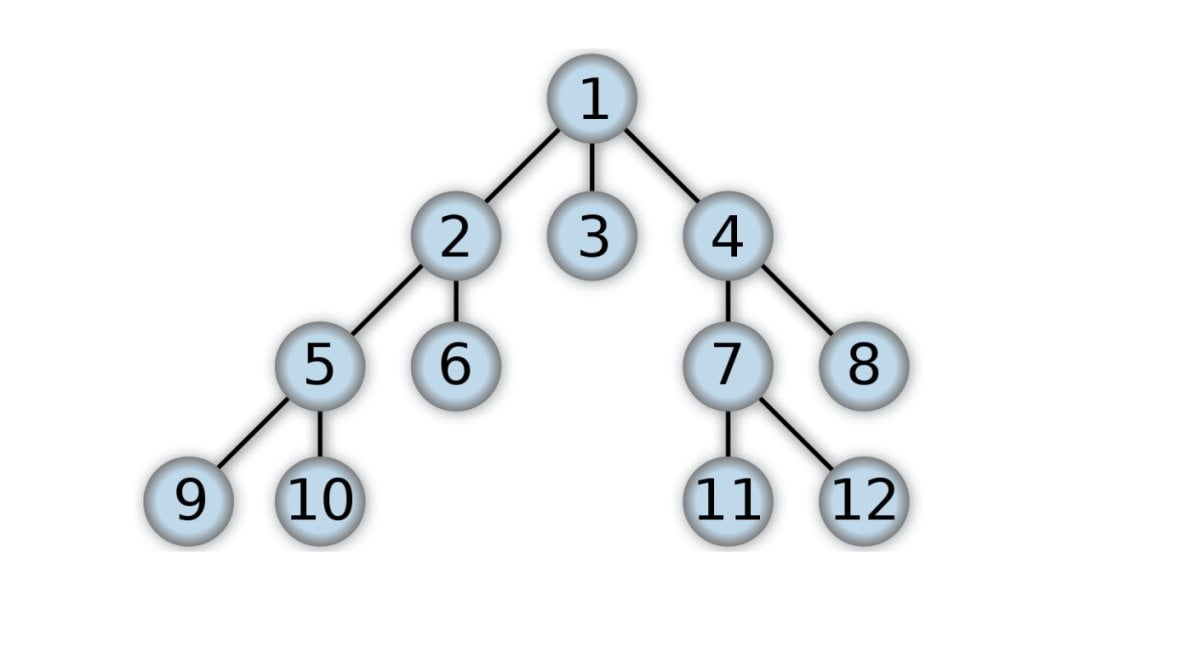
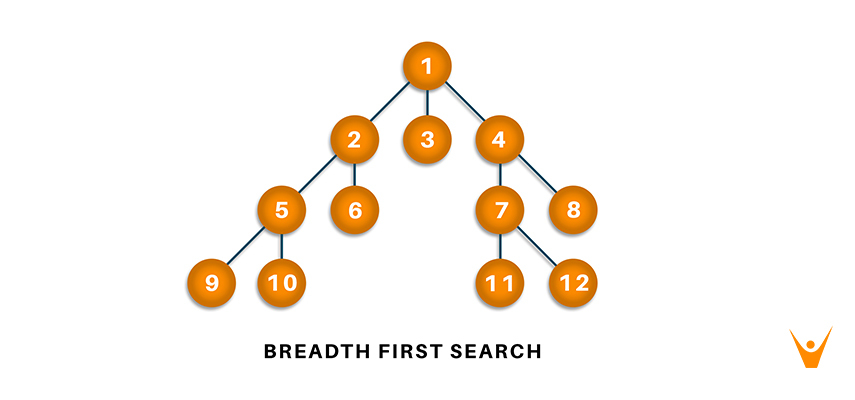
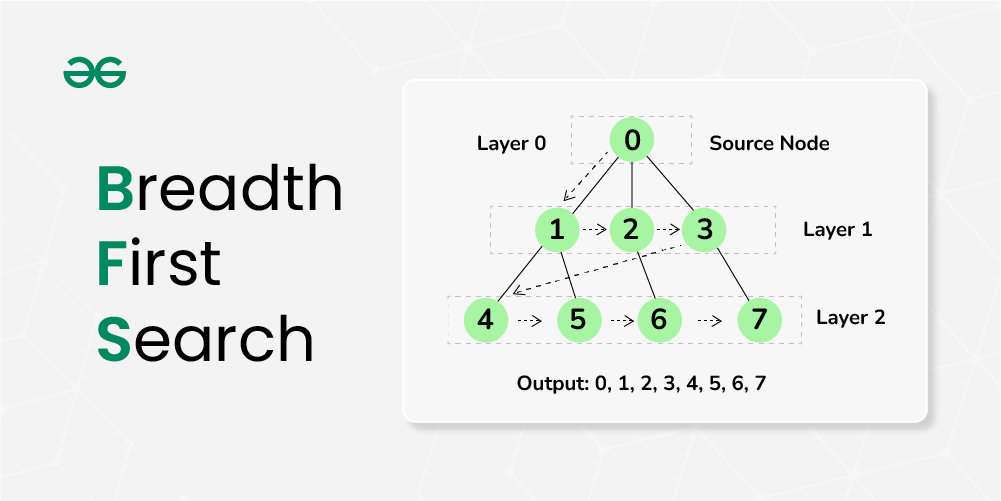
What is breadth-first tree traversal in Python?
Breadth-first tree traversal is a common algorithm used to traverse trees and graphs. In this approach, the algorithm visits all nodes at a given level before moving on to the next level.
Here's an example of how you can implement breadth-first tree traversal in Python using a queue data structure:
from collections import deque
class Node:
def init(self, value):
self.value = value
self.children = []
def breadth_first_traversal(root_node):
if root_node is None:
return
visited_nodes = []
node_queue = deque([root_node])
while node_queue:
current_node = node_queue.popleft()
if current_node not in visited_nodes:
print(current_node.value)
visited_nodes.append(current_node)
for child in current_node.children:
node_queue.append(child)
Example usage
if name == "main":
Create nodes
node1 = Node("Node 1")
node2 = Node("Node 2")
node3 = Node("Node 3")
node4 = Node("Node 4")
Set children for each node
node1.children.append(node2)
node1.children.append(node3)
node2.children.append(node4)
Perform breadth-first traversal
breadth_first_traversal(node1)
In this code:
We define aNode class with properties to hold a value and children. The breadth_first_traversal function takes the root node as an argument. It uses a queue (deque) to keep track of nodes that need to be visited. The algorithm starts by adding the root node to the queue. In each iteration, it dequeues a node, checks if it has been visited before (to avoid infinite loops), prints its value, and marks it as visited. Then it adds all its children to the queue for further processing. This process continues until all nodes have been visited.
The output of this example code would be:
Node 1
Node 2
Node 3
Node 4
This traversal order ensures that we visit all nodes at a given level before moving on to the next level.