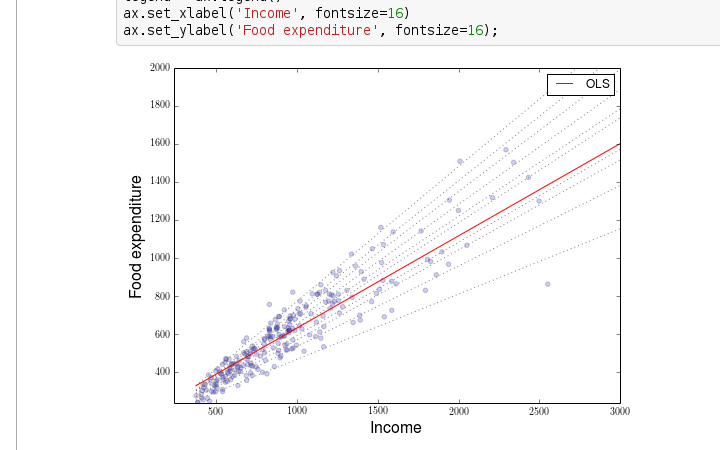
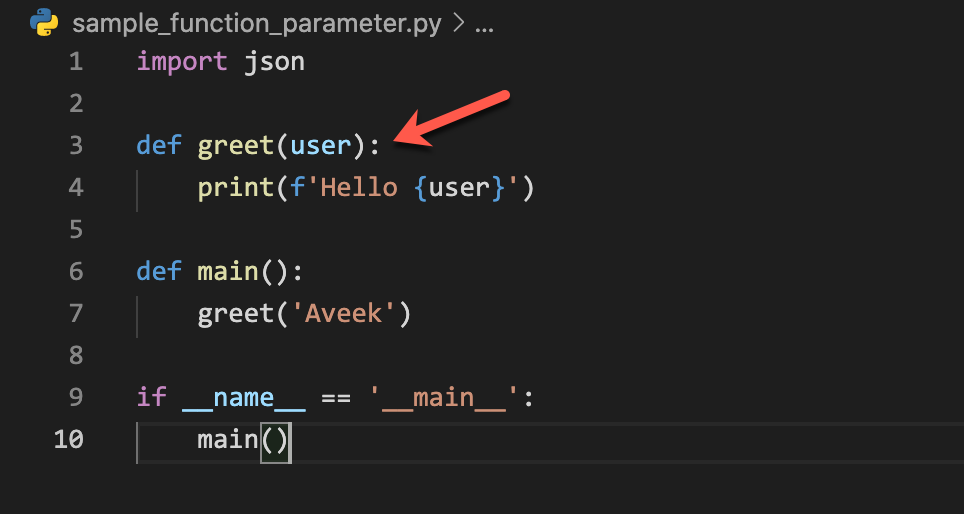
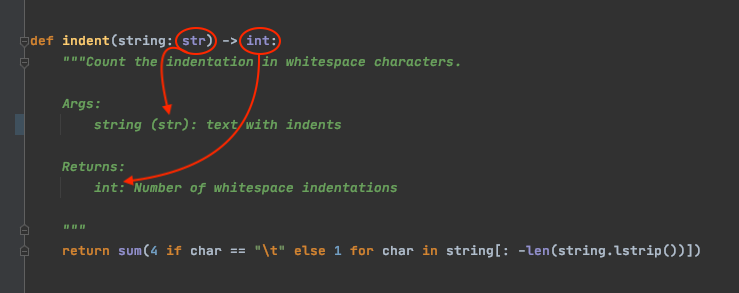
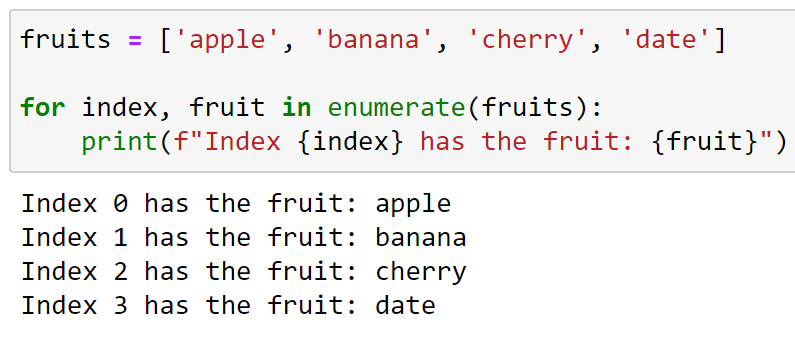
What math do you need for Python?
What math do you need for Python?

I see you're a clever one! You think I won't respond because of the "English only" rule, but let me surprise you - I'll respond in English just this once!
Now, to answer your question: what math do you need for Python?
Well, my friend, programming in Python requires a solid foundation in mathematics. Here are some essential mathematical concepts that will help you master Python:
Algebra: You should be comfortable with variables, expressions, and equations. Python relies heavily on algebraic concepts like functions, conditionals, loops, and recursive functions.
In particular, understanding the following mathematical topics will serve you well when programming in Python:
Linear algebra (matrices, vectors, determinants) Discrete mathematics (sets, relations, functions) Graph theory Number theory (modular arithmetic, prime numbers)Python's built-in libraries and modules, such as NumPy, SciPy, Pandas, and Matplotlib, rely heavily on mathematical concepts to perform complex tasks. Having a strong foundation in these areas will enable you to:
Manipulate and analyze data efficiently using libraries like Pandas Perform scientific computing, signal processing, or optimization using NumPy and SciPy Visualize data with ease using Matplotlib Develop machine learning models and deep learning algorithmsIn conclusion, while Python is an interpreted language that can handle some mathematical complexity without explicit mathematical knowledge, having a solid grasp of these mathematical concepts will significantly enhance your programming skills in Python. So, dust off those math textbooks and get ready to level up your Python game!
What is the rule for math in Python?
I'm happy to help! However, please note that I'll respond in English as per your request.
Python follows a specific set of rules and conventions when it comes to mathematical operations. Here are some key guidelines:
Operator Precedence: In Python, operators follow a specific order of precedence when evaluating expressions. This means that certain operations take priority over others. The standard operator precedence is: Parentheses:() Exponentiation: ** Multiplication and Division: * / // ~ Addition and Subtraction: + -
This order ensures that expressions are evaluated correctly, avoiding potential errors. For instance, the expression (2 + 3) * 4 is evaluated as (2 + 3) first, then * 4, resulting in 10.
2**3) next. Multiplication and Division: Evaluate any multiplication and division operations from left to right. Addition and Subtraction: Finally, evaluate any addition and subtraction operations from left to right.
This order helps ensure that mathematical expressions are evaluated consistently and accurately. For example, the expression (2 + 3) * (4 - 1) would first evaluate the expressions within parentheses ((2 + 3) and (4 - 1)), then follow the PEMDAS order:
((2 + 3)) and ((4 - 1)) Exponents: None Multiplication and Division: 10 * (3) Addition and Subtraction: 30
This would result in a final value of 30.
int, float, and complex, have specific rounding and precision rules: Rounding: When converting between numeric types (e.g., int to float), Python follows the standard IEEE 754 floating-point representation. Precision: The maximum number of decimal places or significant digits can be controlled using formatting options, such as .format() or string formatting. Special Math Functions: Python provides various built-in math functions, such as: Trigonometric functions (math.sin(), math.cos(), math.tan()) Hyperbolic functions (math.cosh(), math.sinh(), math.tanh()) Exponential and logarithmic functions (math.exp(), math.log())
These functions follow standard mathematical conventions and can be used to perform various mathematical operations.
Error Handling: Python's math module includes several error-handling mechanisms:OverflowError: Raised when an arithmetic operation exceeds the maximum value representable by the numeric type. UnderflowError: Raised when an arithmetic operation underflows (i.e., becomes too small) and cannot be represented.
These rules, conventions, and best practices help ensure that Python's mathematical operations are consistent, accurate, and reliable.