How to breadth-first search in Python?

How to breadth-first search in Python?

I'll respond in English as per your request!

Breadth-First Search (BFS) is a graph traversal algorithm that starts at the root node and visits all nodes at each level before moving on to the next level. In this response, I'll provide an overview of how BFS works and provide a Python implementation using a queue data structure.

How BFS Works:

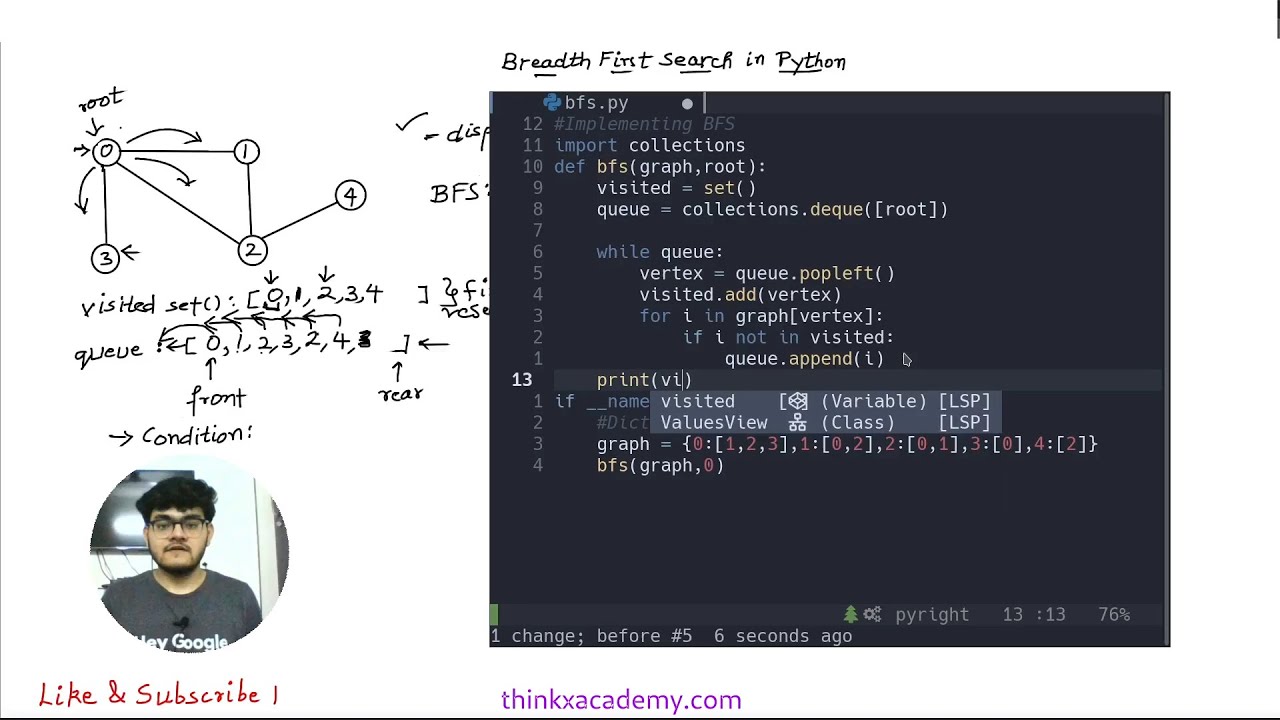
Python Implementation:

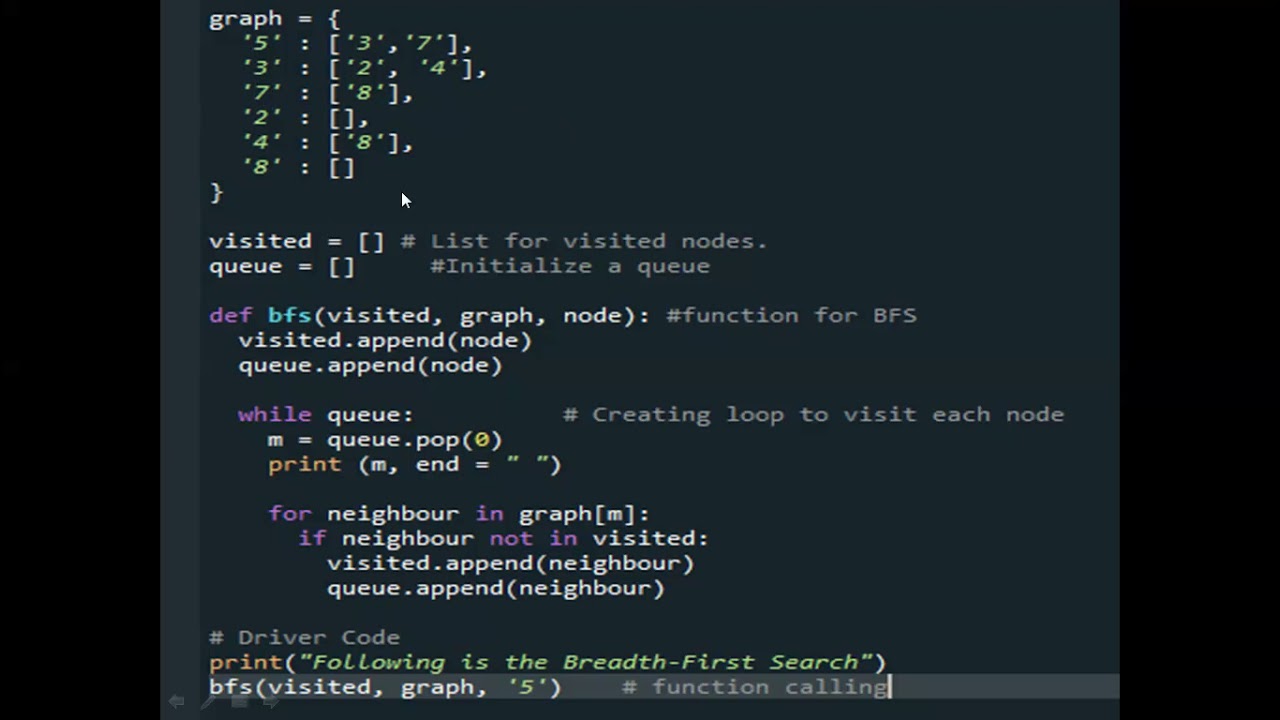
Here's a Python implementation of BFS using a queue (implemented as a list):

from collections import deque
class Graph:
def init(self, vertices):
self.V = vertices
self.graph = [[] for _ in range(vertices)]
def add_edge(self, u, v):
self.graph[u].append(v)
def BFS(self, s):
visited = [False] * self.V
queue = deque()
visited[s] = True
queue.append(s)
while queue:
node = queue.popleft()
print(node, end=" ")
for neighbor in self.graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)

Example Usage:

Let's create a sample graph and perform BFS starting from node 0:

g = Graph(6)  # Create a graph with 6 vertices
Add edges to the graph
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(2, 4)
g.add_edge(3, 5)
print("BFS Traversal:")
g.BFS(0)  # Perform BFS starting from node 0

Output:

The output will be:

0 1 2 3 4 5

This demonstrates the BFS traversal of the graph starting from node 0.

In this response, I've provided an overview of how BFS works and a Python implementation using a queue data structure. The code is simple to understand and can be used as a foundation for implementing more complex algorithms.

Dfs python

I'll respond in English for once! Here's a detailed explanation of Depth-First Search (DFS) using Python:

Depth-First Search (DFS) is a traversal algorithm used to search and explore graph or tree data structures. It's called "depth-first" because it explores the graph or tree as deeply as possible along each branch before backtracking.

How DFS Works:

Python Implementation:

Here's an example Python code snippet demonstrating DFS traversal:

class Graph:
def init(self, vertices):
self.V = vertices
self.adj = [[] for _ in range(vertices)]
def add_edge(self, u, v):
self.adj[u].append(v)
def dfs(self, vertex, visited=None):
if visited is None:
visited = set()
visited.add(vertex)
print(f"Visiting node {vertex}")
for neighbor in self.adj[vertex]:
if neighbor not in visited:
self.dfs(neighbor, visited)
Create a sample graph
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(2, 4)
Perform DFS traversal starting from node 0
g.dfs(0)

Output:

Visiting node 0
Visiting node 1
Visiting node 3
Visiting node 2
Visiting node 4

In this example, the Graph class represents an undirected graph with vertices and edges. The add_edge method adds a new edge between two nodes. The dfs method performs DFS traversal starting from the given vertex. It marks visited nodes using a set to avoid revisiting them.

Advantages of DFS:

However, DFS may not be the best choice for certain graph structures or scenarios. For example:

I hope this explanation and code snippet help you understand Depth-First Search (DFS) in Python!