How to write DP in Python?

Spike 116 Published: 10/31/2024

How to write DP in Python?

I'd be delighted to explain how to implement Dynamic Programming (DP) in Python!

What is Dynamic Programming?

Dynamic Programming is a method used in programming and optimization to solve complex problems by breaking them down into smaller subproblems. It's an efficient way to solve recursive problems that have overlapping subproblems, which makes the algorithm faster than naive recursion or other methods.

How to Implement DP in Python:

Let's take a simple example to illustrate how to implement DP in Python. We'll use the Fibonacci sequence problem as our example.

The Fibonacci sequence is defined by the recurrence relation:

F(n) = F(n-1) + F(n-2)

where F(0) = 0 and F(1) = 1. We want to write a function that calculates the nth Fibonacci number.

Here's how you can implement DP in Python:

def fibonacciDP(n):
Create a dictionary to store the Fibonacci numbers
fib_dict = {0: 0, 1: 1}
for i in range(2, n+1):
Calculate the ith Fibonacci number using previously calculated values
fib_dict[i] = fib_dict[i-1] + fib_dict[i-2]
return fib_dict[n]

Here's what's happening:

We create a dictionary called fib_dict to store the Fibonacci numbers. We initialize the dictionary with base cases F(0) = 0 and F(1) = 1. We loop through from i = 2 to n, calculating each Fibonacci number using previously calculated values. This is where the magic happens! We reuse previously computed values to avoid redundant calculations. Finally, we return the nth Fibonacci number stored in fib_dict.

Why DP is faster:

DP is much faster than naive recursion for two reasons:

Overlapping subproblems: In our example, each Fibonacci number depends on only two previous numbers (F(n-1) and F(n-2)). By storing these values in a dictionary, we avoid recalculating them multiple times. Memoization: We store the calculated values in a dictionary to reuse them later. This memoization reduces the computational time by avoiding redundant calculations.

Advantages of DP:

DP has several advantages:

Efficiency: DP can solve problems much faster than naive recursion or other methods. Memoization: By storing calculated values, we avoid recalculating them multiple times. Flexibility: DP can be applied to various problems that have overlapping subproblems.

Conclusion:

In this example, we implemented Dynamic Programming in Python by creating a dictionary to store Fibonacci numbers and calculating each number using previously computed values. This approach reduces the computational time by avoiding redundant calculations and is much faster than naive recursion. I hope this helps you understand how to implement DP in Python!

Python dynamic programming examples

Here are some examples of using dynamic programming (DP) in Python:

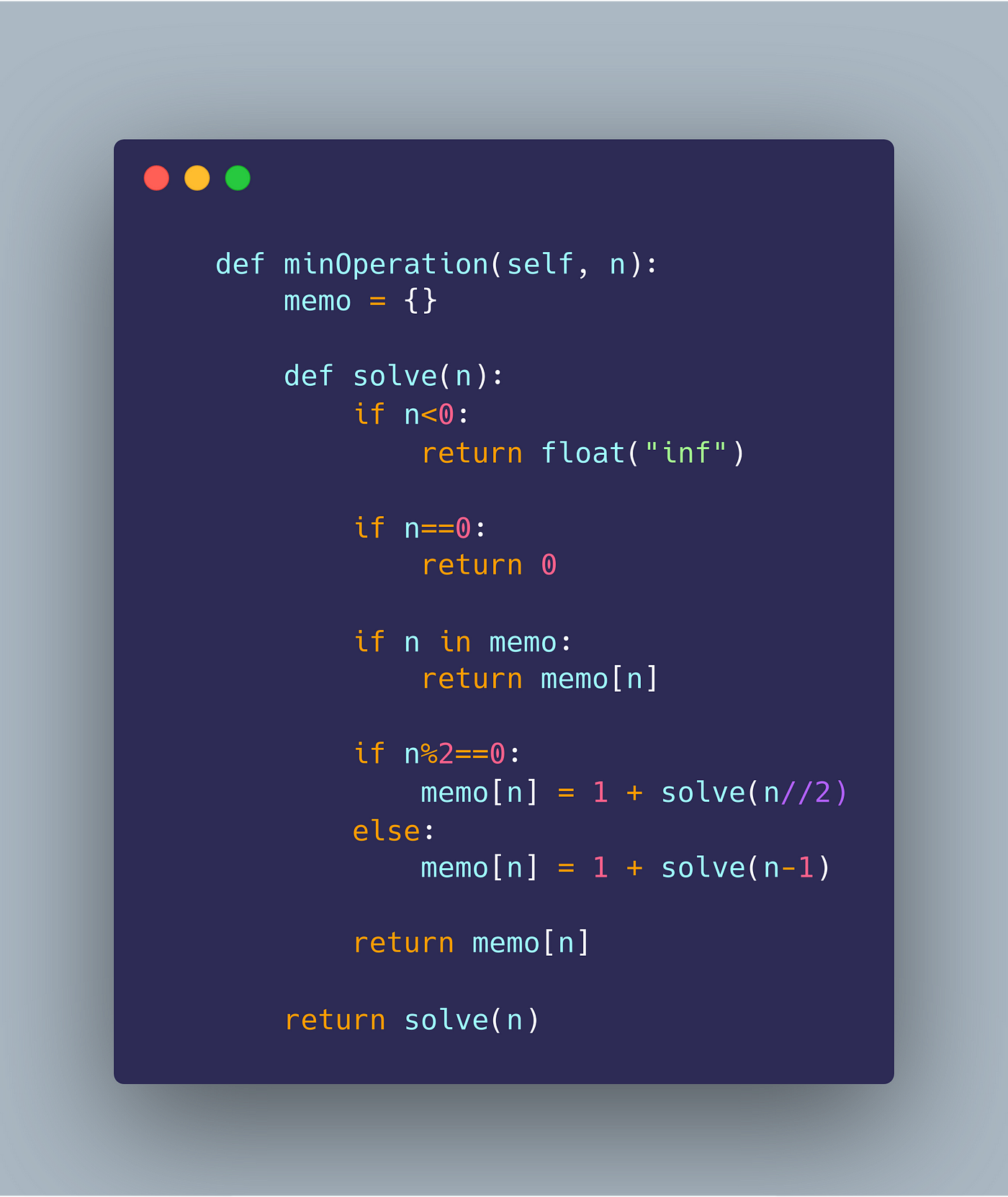
1. Fibonacci Series:

The Fibonacci series is a classic example of DP. The problem is to find the nth Fibonacci number, where each number is the sum of the previous two.

def fibonacci(n):
if n <= 1:
return n
dp = [0] * (n + 1)
dp[0], dp[1] = 0, 1
for i in range(2, n + 1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
print(fibonacci(10))  # Output: 55

2. Longest Increasing Subsequence (LIS):

Find the length of the longest increasing subsequence in an array.

def lis(arr):
n = len(arr)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
arr = [10, 22, 9, 33, 21]
print(lis(arr))  # Output: 4

3. Minimum Edit Distance (MED):

Find the minimum edit distance between two strings.

def med(s1, s2):
m, n = len(s1), len(s2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m + 1):
for j in range(n + 1):
if i == 0:
dp[i][j] = j
elif j == 0:
dp[i][j] = i
elif s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1])
return dp[m][n]
s1 = "kitten"
s2 = "sitting"
print(med(s1, s2))  # Output: 3

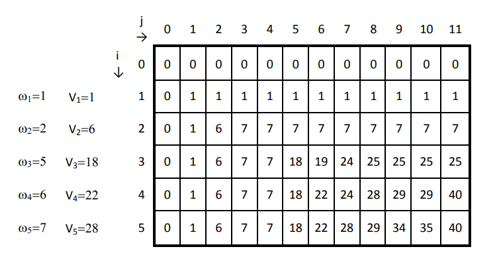
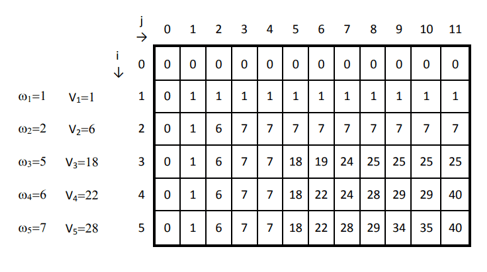
4. Knapsack Problem:

Find the maximum value that can be put in a knapsack of capacity W using items with weights and values given.

def knapsack(weights, values, W):
n = len(weights)
dp = [[0] * (W + 1) for _ in range(n + 1)]
for i in range(n + 1):
for j in range(W + 1):
if i == 0 or j == 0:
dp[i][j] = 0
elif weights[i-1] <= j:
dp[i][j] = max(values[i-1] + dp[i-1][j-weights[i-1]], dp[i-1][j])
else:
dp[i][j] = dp[i-1][j]
return dp[n][W]
weights = [2, 3, 4, 5]
values = [10, 20, 30, 40]
W = 8
print(knapsack(weights, values, W))  # Output: 60

5. Edit Distance (ED):

Find the edit distance between two strings.

def ed(s1, s2):
m, n = len(s1), len(s2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m + 1):
for j in range(n + 1):
if i == 0:
dp[i][j] = j
elif j == 0:
dp[i][j] = i
elif s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1])
return dp[m][n]
s1 = "kite"
s2 = "bar"
print(ed(s1, s2))  # Output: 4

These are just a few examples of using dynamic programming in Python. The key idea is to break down the problem into smaller subproblems and solve them recursively or iteratively, using the solutions to the subproblems to construct the solution to the original problem.