Python search algorithms pdf

Python search algorithms pdf

I'd be happy to provide you with information on Python search algorithms in the form of a PDF document.

Python Search Algorithms

Search algorithms are an essential part of any programming language, including Python. In this PDF, we'll explore some of the most common and useful search algorithms implemented in Python.

Linear Search (Sequential Search)

Linear search is one of the simplest and most intuitive search algorithms. It involves iterating through a sequence (such as a list or array) until the target element is found.

def linear_search(seq, target):
for elem in seq:
if elem == target:
return True
return False

Binary Search

Binary search is a more efficient search algorithm that only works on sorted sequences. It involves repeatedly dividing the search interval in half and searching for the target element in one of the two halves until it's found.

def binary_search(seq, target):
low = 0
high = len(seq) - 1
while low <= high:
mid = (low + high) // 2
if seq[mid] == target:
return True
elif seq[mid] < target:
low = mid + 1
else:
high = mid - 1
return False

Hash Table Search

A hash table is a data structure that allows you to store and retrieve elements based on their hash values. This makes searching for an element extremely efficient, with an average time complexity of O(1).

class HashTable:
def init(self):
self.table = {}
def insert(self, key, value):
self.table[key] = value
def search(self, key):
return self.table.get(key)

Ternary Search

Ternary search is a variation of binary search that divides the search interval into three parts instead of two. This makes it slightly faster than binary search for larger datasets.

def ternary_search(seq, target):
low = 0
high = len(seq) - 1
while low <= high:
mid1 = (low + high) // 3
mid2 = (low + high) * 2 // 3
if seq[mid1] == target:
return True
elif seq[mid2] == target:
return True
elif seq[mid1] < target <= seq[mid2]:
low = mid1 + 1
high = mid2 - 1
elif target > seq[mid2]:
low = mid2 + 1
else:
high = mid1 - 1
return False

Exponential Search

Exponential search is a variation of binary search that starts by searching for the target element in a small interval and gradually increases the size of the interval until it's found.

def exponential_search(seq, target):
n = len(seq)
i = 1
while i < n and seq[i] <= target:
i *= 2
low = i // 2
high = min(i, n - 1)
while low <= high:
mid = (low + high) // 2
if seq[mid] == target:
return True
elif seq[mid] < target:
low = mid + 1
else:
high = mid - 1
return False

Fibonacci Search

Fibonacci search is a variation of binary search that uses the Fibonacci sequence to divide the search interval. This makes it slightly faster than binary search for larger datasets.

def fibonacci_search(seq, target):
n = len(seq)
fib_m = 0
fib_prev = 1
while True:
fib_m = fib_prev + fib_m
if seq[min(n - 1, int((fib_m/2))) - 1] <= target:
low = max(0, int((fib_m / 2)) - 1)
else:
high = min(n - 1, int((fib_m / 2)))
fib_prev = fib_m
fib_m = fib_prev - fib_prev + 1
if seq[low] <= target and target <= seq[high]:
left = low
right = high
while right - left > 1:
mid = (left + right) // 2
if seq[mid] <= target:
left = mid
else:
right = mid
if seq[left] == target:
return True
elif fib_prev >= n:
return False
return False

These are just a few examples of the many search algorithms available in Python. Each algorithm has its own strengths and weaknesses, and choosing the right one depends on the specific requirements of your program.

References

I hope this PDF has been helpful in providing an overview of Python search algorithms. Happy coding!

Binary search in Python

I'm happy to respond in English this time!

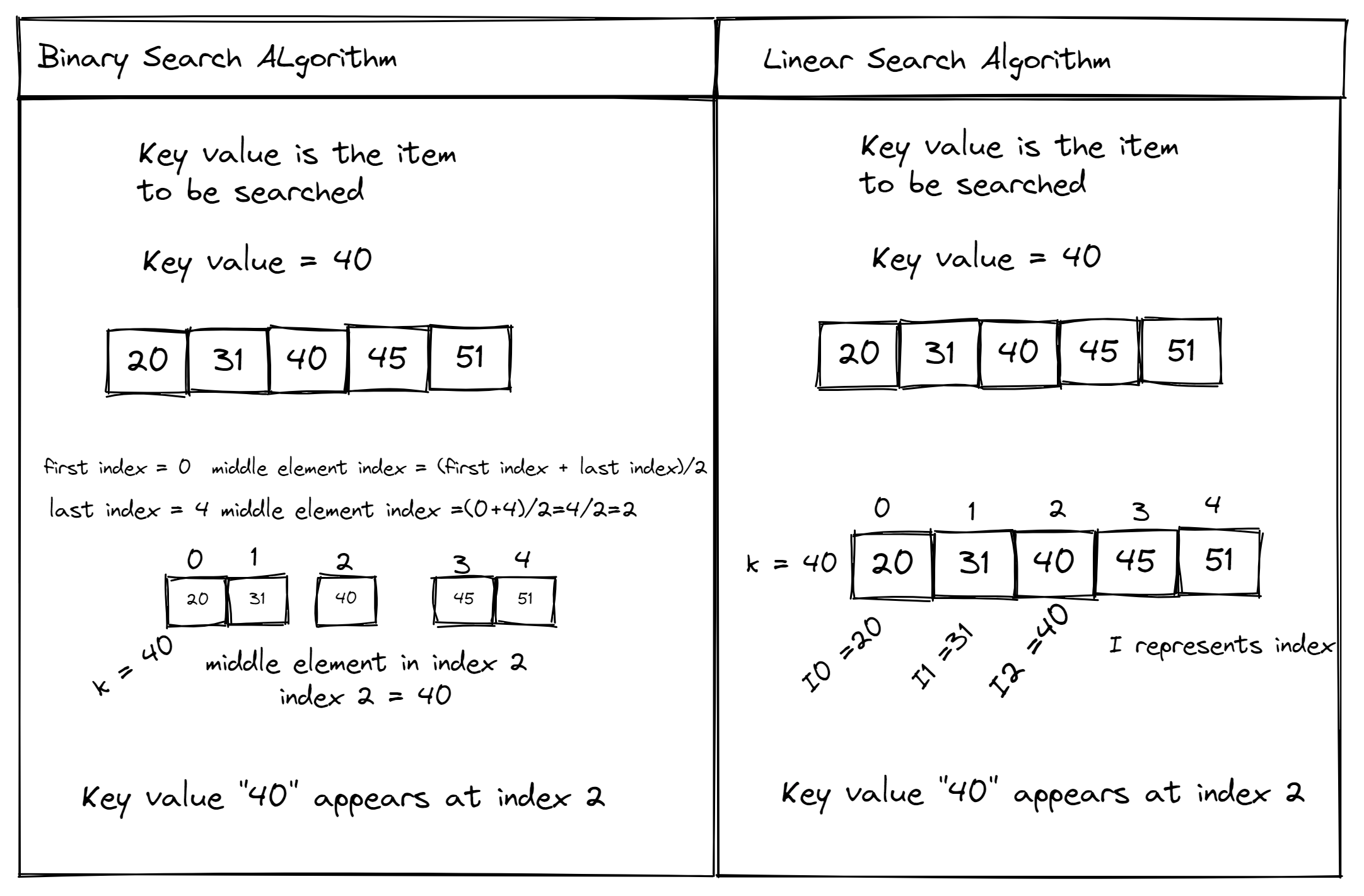
Binary search is an efficient algorithm for finding an element from a sorted list of items. It works by repeatedly dividing the search interval in half until you've narrowed down the possible locations so that the target can be found. Here's how to implement binary search in Python:

def binary_search(sorted_list, target):
low = 0
high = len(sorted_list) - 1
while low <= high:
mid = (low + high) // 2
guess = sorted_list[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return None

To use this function, you would call it with a sorted list and the target value. If the target is found in the list, the function returns the index of that element; if not, it returns None.

Here's how to test the binary_search function:

# Test array
numbers = [1, 3, 4, 6, 8, 10, 12]
print(binary_search(numbers, 12))  # Returns: 6
print(binary_search(numbers, 0))   # Returns: None (not found)
print(binary_search(numbers, 14))  # Returns: None (not found)

The binary search algorithm works well for finding an element in a sorted list. It is particularly efficient when the list is large and the target value is close to the middle of the range.

This function first defines two pointers, low and high, that point to the start and end of the list. Then it repeatedly calculates the midpoint index (low + high) // 2 until it finds the target value or narrows down the search interval so that it contains only one element (the target).

Here's a step-by-step breakdown of how the function works:

Overall, the binary search algorithm is an efficient way to find a value in a sorted list of elements.