Python dynamic programming tutorial

Python dynamic programming tutorial

I'd be happy to provide a Python dynamic programming tutorial for you.

What is Dynamic Programming?

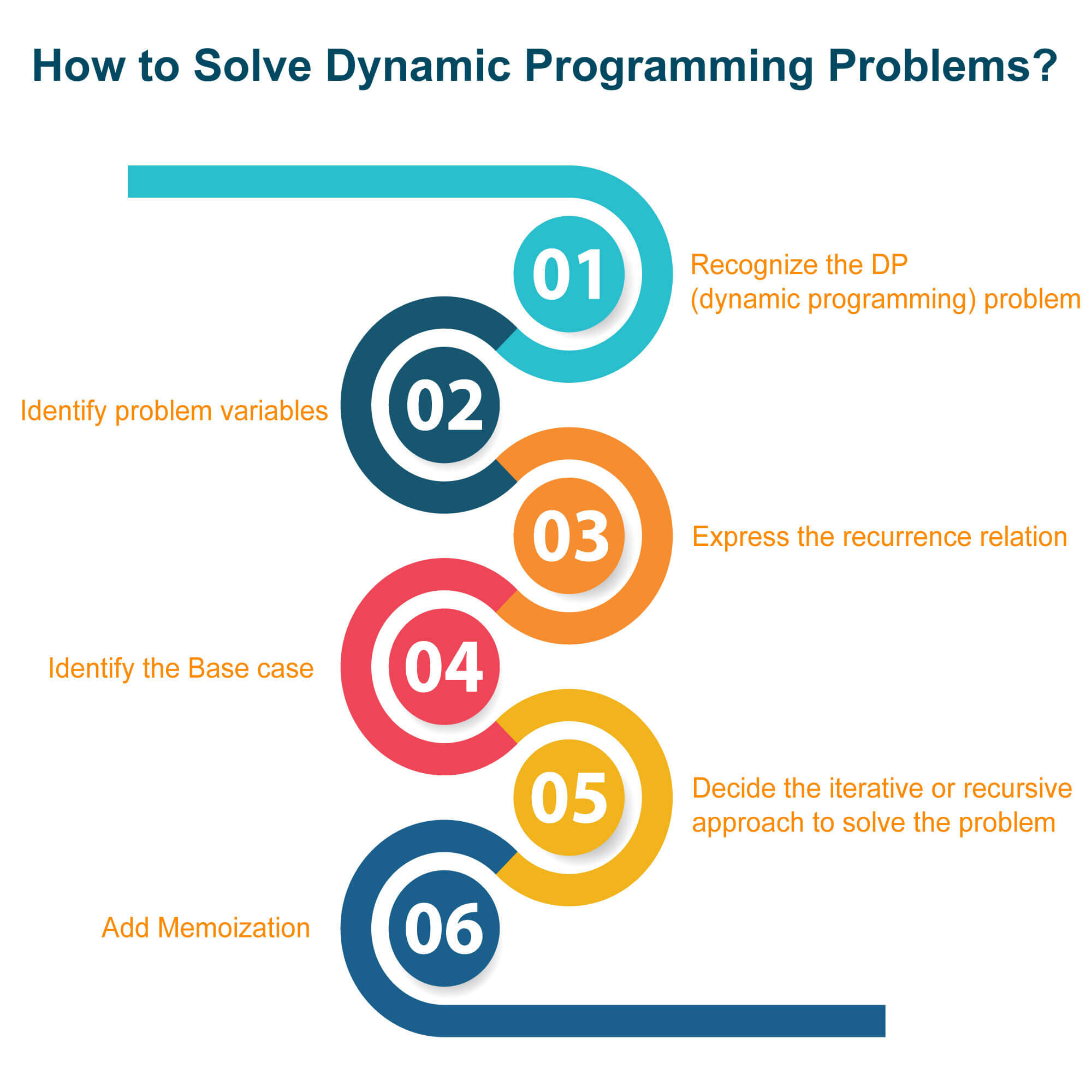
Dynamic programming is a method for solving complex problems by breaking them down into smaller subproblems, which can be solved independently and reused when needed. This approach is particularly useful when the problem has overlapping subproblems or when the solution depends on previous solutions.

Why Use Dynamic Programming?

There are several reasons why dynamic programming is valuable:

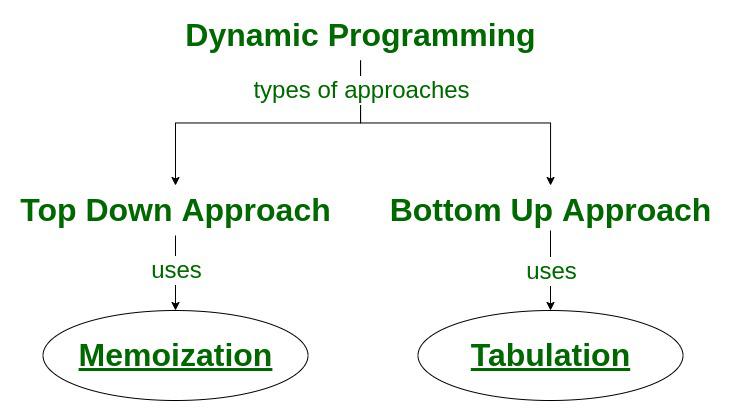
A Basic Example: Fibonacci Sequence

The Fibonacci sequence is a classic example of dynamic programming. The sequence starts with 0 and 1, and each subsequent number is the sum of the previous two (1, 1, 2, 3, 5, 8, 13, ...).

Here's a naive implementation in Python:

def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)

This code has exponential time complexity because it recalculates the same Fibonacci numbers multiple times. We can improve this by using dynamic programming.

Dynamic Programming Implementation:

We create a table fib to store the computed Fibonacci numbers and initialize it with the base cases (0 and 1). Then, we fill up the table row by row, using previously computed values:

def fibonacci(n):
fib = [0] * (n + 1)
fib[0] = 0
fib[1] = 1
for i in range(2, n+1):
fib[i] = fib[i-1] + fib[i-2]
return fib[n]

This implementation has linear time complexity because we only compute each Fibonacci number once and store it in the table.

Other Examples:

Dynamic programming can be applied to many problems, such as:

These problems can be solved using dynamic programming by breaking them down into smaller subproblems, solving each one only once, and storing the results for later use.

Conclusion:

Dynamic programming is a powerful technique for solving complex problems efficiently. By breaking down the problem into smaller subproblems, we reduce redundant computations and store the results to avoid recalculations. This approach is particularly useful when the solution depends on previous solutions or has overlapping subproblems. With practice, you can master dynamic programming and tackle a wide range of computational challenges.

I hope this tutorial has given you a solid understanding of dynamic programming in Python!

Dynamic programming Python github

I'd be happy to help!

Dynamic programming is an optimization technique used primarily for solving complex problems by breaking them down into smaller subproblems. It's a powerful approach that can solve problems that would be difficult or impossible to solve using traditional algorithms.

In the context of Python, dynamic programming can be implemented using various techniques such as memoization and tabulation. Memoization involves storing the results of expensive function calls and reusing them when the same inputs occur again. Tabulation, on the other hand, involves building a table of solutions to subproblems and reusing those solutions to solve larger problems.

One popular example of dynamic programming is Fibonacci sequence calculation. The traditional recursive approach would involve calculating each Fibonacci number by adding the two preceding numbers, which leads to an exponential time complexity. By using memoization or tabulation, we can reduce the time complexity to linear, making it much more efficient.

Here's a simple implementation of dynamic programming in Python for calculating the Fibonacci sequence:

def fib(n, memo={}):
if n <= 0:
return 0
elif n == 1:
return 1
elif n not in memo:
memo[n] = fib(n-1, memo) + fib(n-2, memo)
return memo[n]

This function uses a dictionary memo to store the results of previously calculated Fibonacci numbers. When calculating the nth Fibonacci number, it checks if the result is already stored in memo. If so, it returns the cached result instead of recalculating it.

Another popular example is the Longest Common Subsequence (LCS) problem. Given two sequences, we want to find the longest subsequence that appears in both. This can be solved using dynamic programming by building a 2D table where each cell represents the length of the LCS for the corresponding subsequences.

Here's an implementation of the LCS problem in Python:

def lcs(X,Y):
m=len(X)
n=len(Y)
L=[[0]*(n+1) for i in range(m+1)]
longest=0
for i in range(m+1):
for j in range(n+1):
if i == 0:
L[i][j] = 0
elif j == 0:
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1]+1
if longest < L[i][j]:
longest=L[i][j]
return longest

This function uses a 2D table L to store the lengths of the LCS for the corresponding subsequences. The outer loop iterates over the elements of sequence X, and the inner loop iterates over the elements of sequence Y. When matching characters are found in both sequences, the length of the LCS is incremented, and if this exceeds the previous longest LCS length, it's updated.

Dynamic programming has many applications in computer science, including algorithmic game theory, computational biology, and machine learning. By breaking down complex problems into smaller subproblems, dynamic programming provides a powerful tool for solving problems that would be difficult or impossible to solve using traditional algorithms.

If you're interested in learning more about dynamic programming, I highly recommend checking out the GitHub repository by David Eppstein, which contains many examples and explanations of dynamic programming in Python: https://github.com/eppsteindp/

References:

[1] https://www.geeksforgeeks.org/dynamic-programming-set-10-fibonacci-series/

[2] https://www.programiz.com/python-program-snippets/python-dynamic-programming

Let me know if you have any further questions!