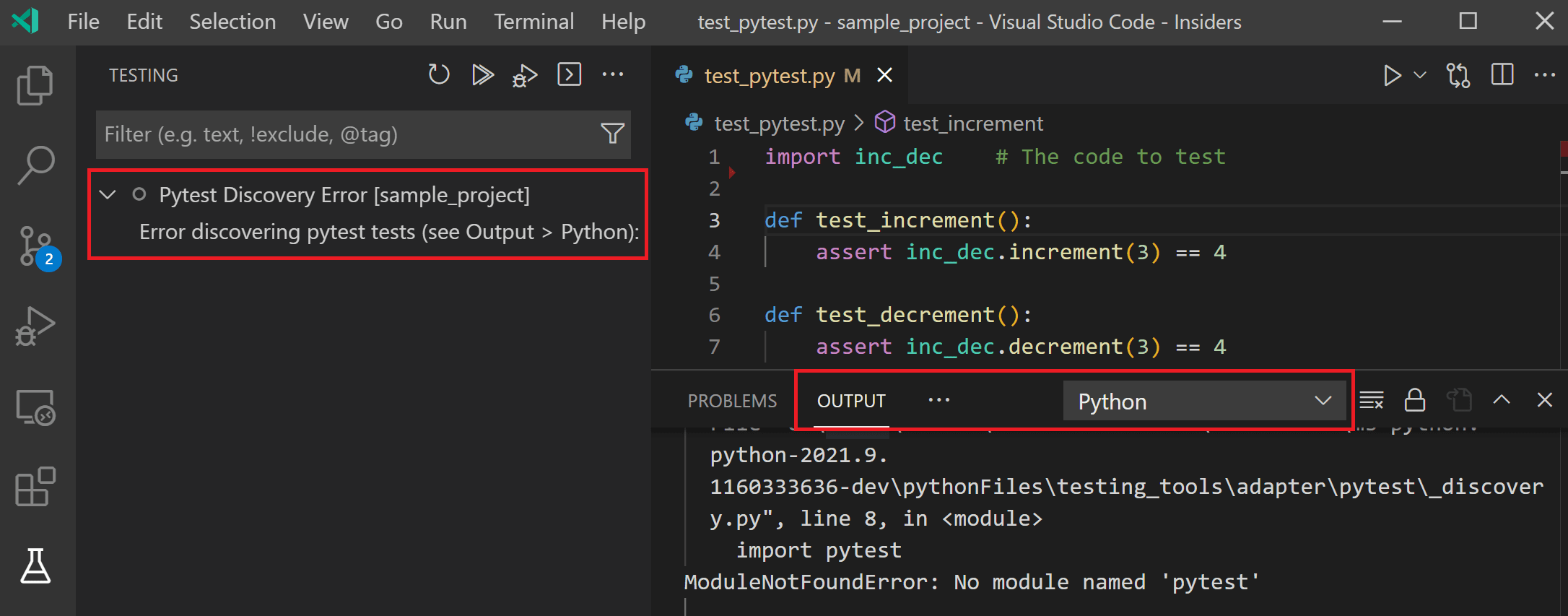
Is there a binary search in Python?

Is there a binary search in Python?

I'm glad you asked! Yes, there are several ways to implement binary search in Python. In this answer, I'll cover the most common approaches.

The Classic Binary Search Algorithm

Before diving into Python-specific implementations, let's start with a brief overview of the classic binary search algorithm:

Given an array arr of size n, where all elements are unique and sorted in ascending order, find the index of a target value target.

This process continues until the target value is found or it's determined that the target value is not in the array (i.e., low > high).

Python Implementations

Now, let's explore Python-specific implementations of binary search:

You can implement a simple binary search algorithm using recursion:

def binary_search(arr, target):
low = 0
high = len(arr) - 1
def recursive_search(low, high):
if low > high:
return -1  # Not found
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
return recursive_search(mid + 1, high)
else:
return recursive_search(low, mid - 1)
return recursive_search(low, high)

This implementation uses a recursive function to perform the search.

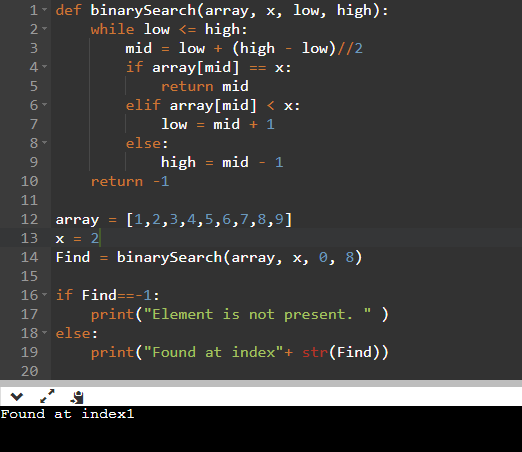
You can also implement an iterative binary search algorithm using a loop:

def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1  # Not found

This implementation uses a while loop to perform the search.

Python's built-in bisect module provides a more convenient way to implement binary search. The bisect_left and bisect_right functions can be used to find the insertion point of a target value in a sorted array.

import bisect
def binary_search(arr, target):
idx = bisect.bisect_left(arr, target)
if idx != len(arr) and arr[idx] == target:
return idx
return -1  # Not found

This implementation is concise and easy to use.

The performance of these implementations depends on the size of the input array and the target value. In general, the iterative implementation (Method 2) tends to be slightly faster than the recursive implementation (Method 1). The bisect module-based implementation (Method 3) is often the fastest, as it leverages CPython's optimized binary search algorithm.

In conclusion, Python provides various ways to implement binary search. Choose the approach that best suits your needs and constraints.

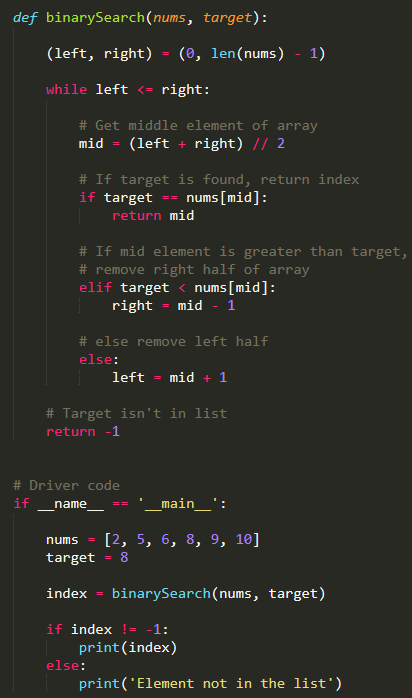
Python binary search example

Here is an example of a Python program that uses the binary search algorithm to find a target value in a sorted list:

def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
Test the function
arr = [1, 3, 5, 7, 9]
target = 8
result = binary_search(arr, target)
if result != -1:
print("Target value found at index", result)
else:
print("Target value not found in the array")

This program defines a function called binary_search that takes two parameters: arr, which is the sorted list to search through, and target, which is the value we are trying to find. The function uses the binary search algorithm to efficiently search for the target value.

The algorithm starts by initializing two variables: low and high. These variables represent the range of indices in the array that we should consider searching within. Initially, this range is set to be the entire array (i.e., from index 0 up to and including the last index).

Next, the function calculates the midpoint of the current range using the expression (low + high) // 2. This is a simple way to calculate the midpoint without worrying about integer division.

The function then checks whether the value at the midpoint index matches the target value. If it does, the function returns the index of the target value.

If the value at the midpoint index is less than the target value, this means that the target value must be located in the upper half of the current range. In this case, we update the low variable to be equal to the midpoint index plus 1, effectively moving the lower bound of our search range up one step.

On the other hand, if the value at the midpoint index is greater than the target value, this means that the target value must be located in the lower half of the current range. In this case, we update the high variable to be equal to the midpoint index minus 1, effectively moving the upper bound of our search range down one step.

This process continues until we find the target value (in which case we return its index) or until the range is empty (in which case we conclude that the target value was not found in the array).

The test at the end of the program uses this binary_search function to search for the value 8 in a sample sorted list.