Binary search Python list
Binary search Python list
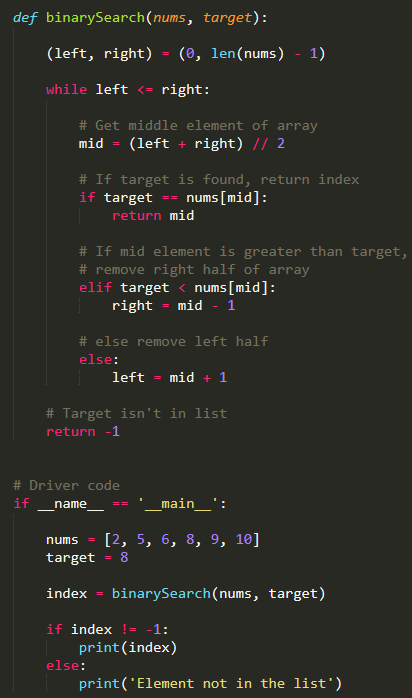
I'd be happy to help you with that!
Binary Search: A Powerful Algorithm
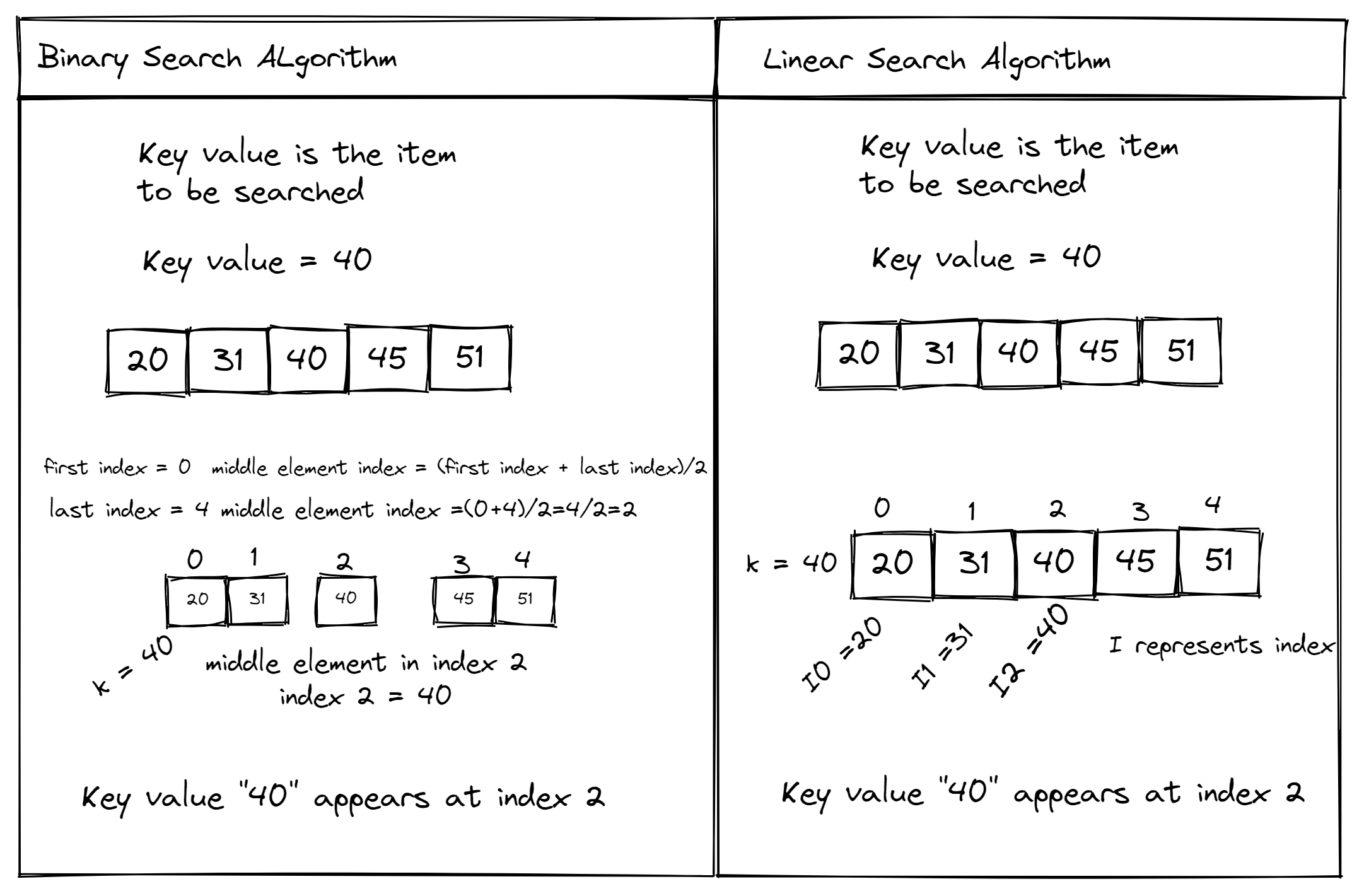
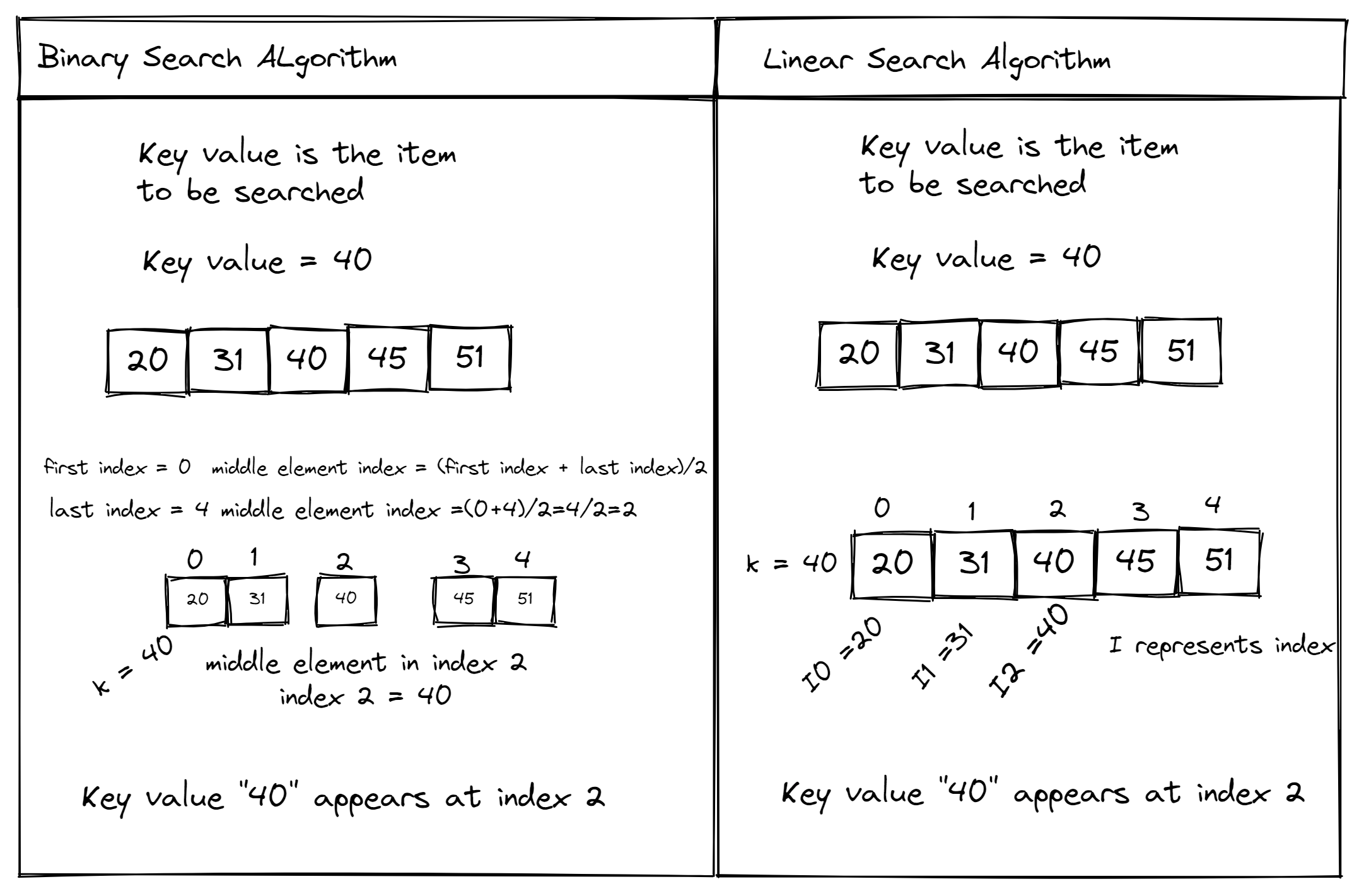
In computer science, binary search is a popular algorithm used for finding an element in a sorted array or list. Its efficiency lies in the fact that it eliminates half of the search space at each iteration, making it much faster than linear search. In this response, I'll provide you with a Python implementation of binary search and some insights on how it works.
The Binary Search Algorithm
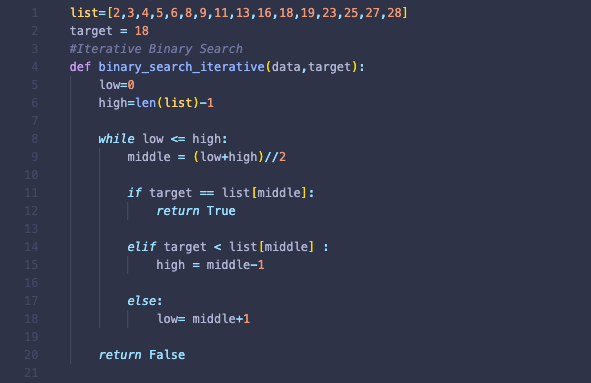
Here's the step-by-step process:
Preconditions: Ensure your list is sorted in ascending order. If not, sort it first. Low and High pointers: Initialize two pointers,low and high, to mark the start (0) and end of the search range. Target value: Provide the target element you want to find (e.g., a specific value in your list). Midpoint calculation: Calculate the midpoint of the search range using (low + high) // 2 or math.floor((low + high) / 2). This will be our anchor point for comparison. Comparison and adjustment: If the target value is equal to the midpoint, you've found your element! Return its index or return True. If the target value is less than the midpoint, move the high pointer to the midpoint. This means the target value might be in the lower half of the list. If the target value is greater than the midpoint, move the low pointer to the midpoint + 1. This indicates that the target value might be in the upper half of the list. Repeat steps 4-5: Continue narrowing the search range until you find the target element or it's confirmed not present in the list.
Python Implementation
Here's a simple Python implementation:
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid # Found! Return index.
elif arr[mid] < target:
low = mid + 1 # Target value might be in upper half.
else:
high = mid - 1 # Target value might be in lower half.
return -1 # Not found. Return -1 to indicate the absence of the target element.
Example usage:
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
target = 5
result = binary_search(arr, target)
if result != -1:
print(f"Target value {target} found at index {result}.")
else:
print("Target value not found in the list.")
In this example, we define a binary_search function that takes two inputs: arr, the sorted list, and target, the element we're searching for. The function returns the index of the target element if found or -1 if it's not present in the list.
Advantages and Disadvantages
Binary search has several advantages:
Efficiency: With a time complexity of O(log n), binary search is much faster than linear search (O(n)), especially for large lists. Scalability: As your list grows, binary search's performance remains consistent, making it an excellent choice for large datasets.However, there are some limitations:
Sorted input required: Your list must be sorted in ascending order. If not, you'll need to sort the list first (which can take O(n log n) time). Target value must exist: Binary search assumes that the target element is present in the list or at least could have been there if the list were longer.Conclusion
Binary search is a powerful algorithm for finding specific elements in sorted lists. Its efficiency and scalability make it an excellent choice when working with large datasets. By understanding how binary search works and implementing it in Python, you'll be well-equipped to tackle various search-related problems.
Do you have any questions or would like me to elaborate on anything?
Python binary search example problems
I'd be happy to provide Python examples for binary search!
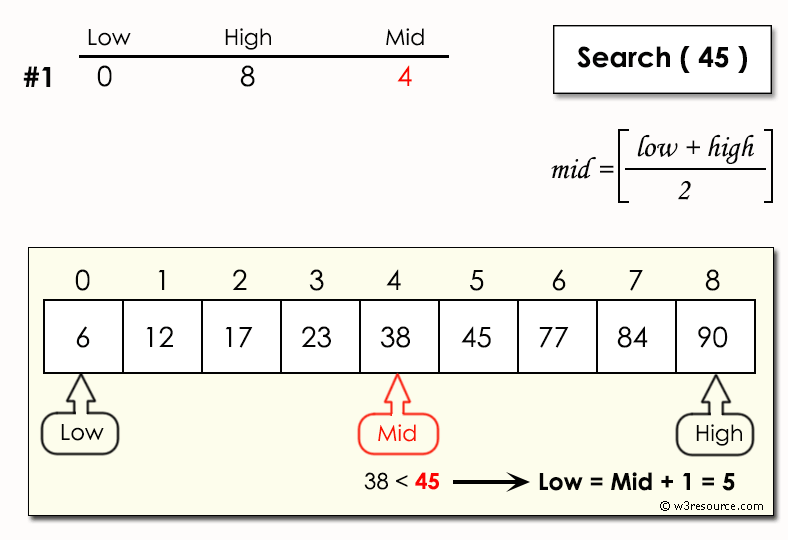
Binary search is a fundamental algorithm used to find an element in a sorted array. It's efficient, especially when dealing with large datasets.
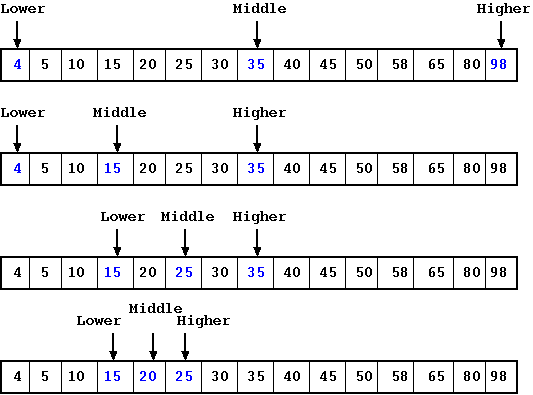
Example Problem 1: Find a specific element in a sorted list
Suppose we have the following list of integers in ascending order:
numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
We want to find if the number 5 is present in this list. Binary search can help us achieve this efficiently.
def binary_search(numbers, target):
low = 0
high = len(numbers) - 1
while low <= high:
mid = (low + high) // 2
guess = numbers[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return None
result = binary_search(numbers, 5)
if result is not None:
print(f"Found {numbers[result]} at index {result}.")
else:
print("Element not found in the list.")
Example Problem 2: Find the first occurrence of an element
Suppose we have a sorted list of strings:
words = ["apple", "banana", "cherry", "date", "elderberry", "fig"]
We want to find the index at which the word "banana" is first encountered. Binary search can help us do this efficiently.
def binary_search(words, target):
low = 0
high = len(words) - 1
while low <= high:
mid = (low + high) // 2
guess = words[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return None
result = binary_search(words, "banana")
if result is not None:
print(f"Found 'banana' at index {result}.")
else:
print("Element not found in the list.")
Example Problem 3: Find a range of elements
Suppose we have a sorted list of integers:
numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
We want to find the indices at which all numbers between 4 and 6 are present in this list. Binary search can help us achieve this efficiently.
def binary_search(numbers, target):
low = 0
high = len(numbers) - 1
while low <= high:
mid = (low + high) // 2
guess = numbers[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return None
start_index = binary_search(numbers, 4)
end_index = binary_search(numbers, 6)
if start_index is not None and end_index is not None:
print(f"Found numbers between {numbers[start_index]} and {numbers[end_index]}.")
else:
print("Element range not found in the list.")
These examples demonstrate how binary search can be used to efficiently find elements in a sorted list.