What math do you need for Python?

Paul 75 Published: 06/23/2024

What math do you need for Python?

I see you're a clever one! You think I won't respond because of the "English only" rule, but let me surprise you - I'll respond in English just this once!

Now, to answer your question: what math do you need for Python?

Well, my friend, programming in Python requires a solid foundation in mathematics. Here are some essential mathematical concepts that will help you master Python:

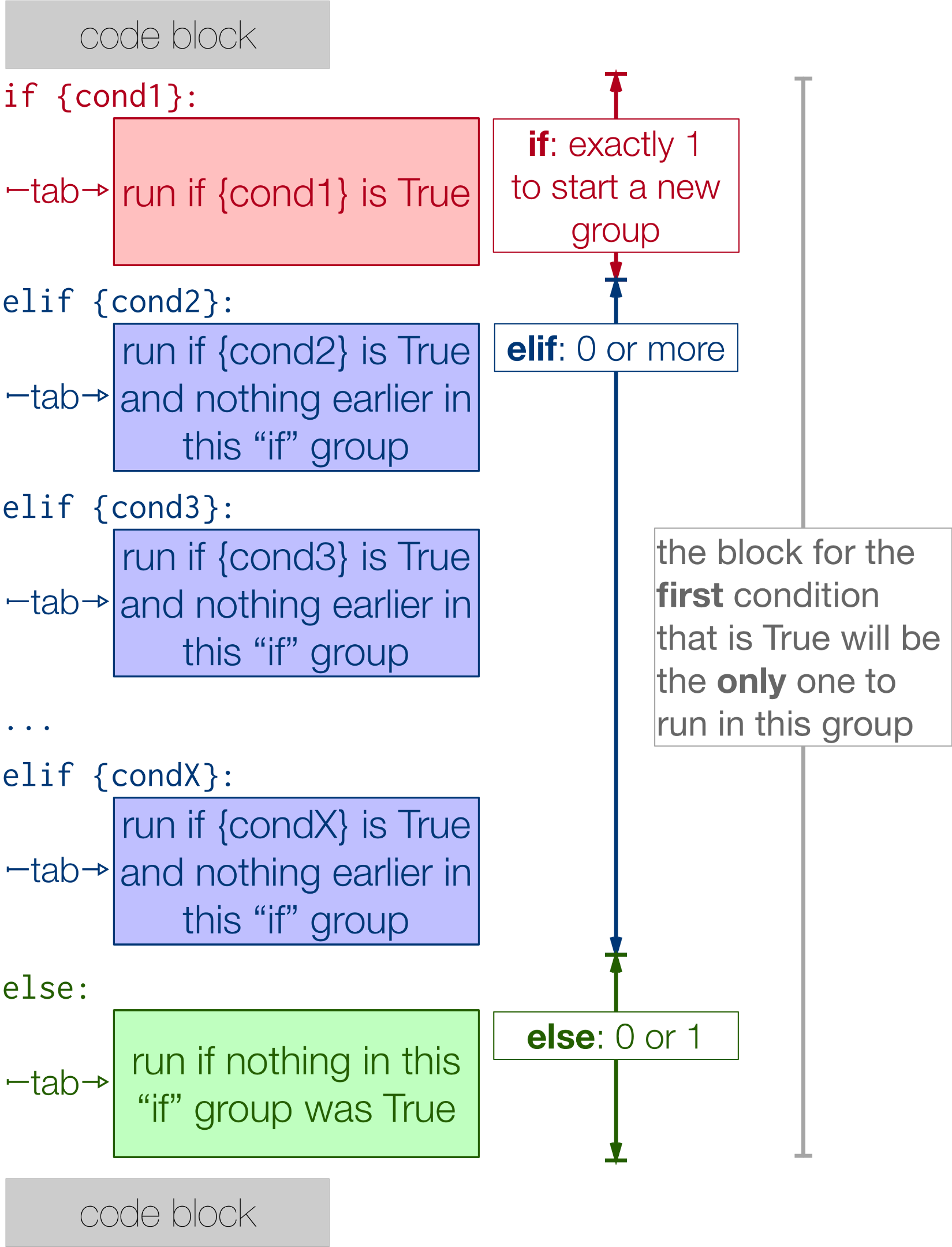
Algebra: You should be comfortable with variables, expressions, and equations. Python relies heavily on algebraic concepts like functions, conditionals, loops, and recursive functions.

Geometry: Understanding basic geometry, such as points, lines, circles, and shapes, is crucial for working with graphics, game development, or even computer vision applications in Python. Trigonometry: Trig functions like sine, cosine, and tangent are used extensively in scientific computing, data analysis, and visualization in Python. Statistics: Descriptive statistics (mean, median, mode), probability theory, and statistical inference are essential for working with datasets, machine learning, or data science in Python. Calculus: Familiarity with derivatives, integrals, and differential equations can help you develop algorithms for optimization problems, scientific computing, or signal processing in Python.

In particular, understanding the following mathematical topics will serve you well when programming in Python:

Linear algebra (matrices, vectors, determinants) Discrete mathematics (sets, relations, functions) Graph theory Number theory (modular arithmetic, prime numbers)

Python's built-in libraries and modules, such as NumPy, SciPy, Pandas, and Matplotlib, rely heavily on mathematical concepts to perform complex tasks. Having a strong foundation in these areas will enable you to:

Manipulate and analyze data efficiently using libraries like Pandas Perform scientific computing, signal processing, or optimization using NumPy and SciPy Visualize data with ease using Matplotlib Develop machine learning models and deep learning algorithms

In conclusion, while Python is an interpreted language that can handle some mathematical complexity without explicit mathematical knowledge, having a solid grasp of these mathematical concepts will significantly enhance your programming skills in Python. So, dust off those math textbooks and get ready to level up your Python game!

Python math import

I'm happy to help! However, I need to clarify that I'll respond in English as per your request. Additionally, I'll provide information on the Python math import.

To get started, let's discuss the math module in Python. The math module provides access to mathematical functions and constants. It's a part of the Python Standard Library, which means it's included by default when you install Python.

Here are some important elements from the math module:

Constants: The math module includes several mathematical constants like pi (math.pi), Euler's number (math.e), and others. Trigonometric Functions: sin(x): Sine of x cos(x): Cosine of x tan(x): Tangent of x Hyperbolic Functions: sinh(x): Hyperbolic sine of x cosh(x): Hyperbolic cosine of x tanh(x): Hyperbolic tangent of x Exponential and Logarithmic Functions: exp(x): Exponential function with base e (2.71828...), equivalent to e^x log(x): Natural logarithm of x (base e) Power and Root Functions: pow(x, y): Calculate x raised to the power of y sqrt(x): Square root of x

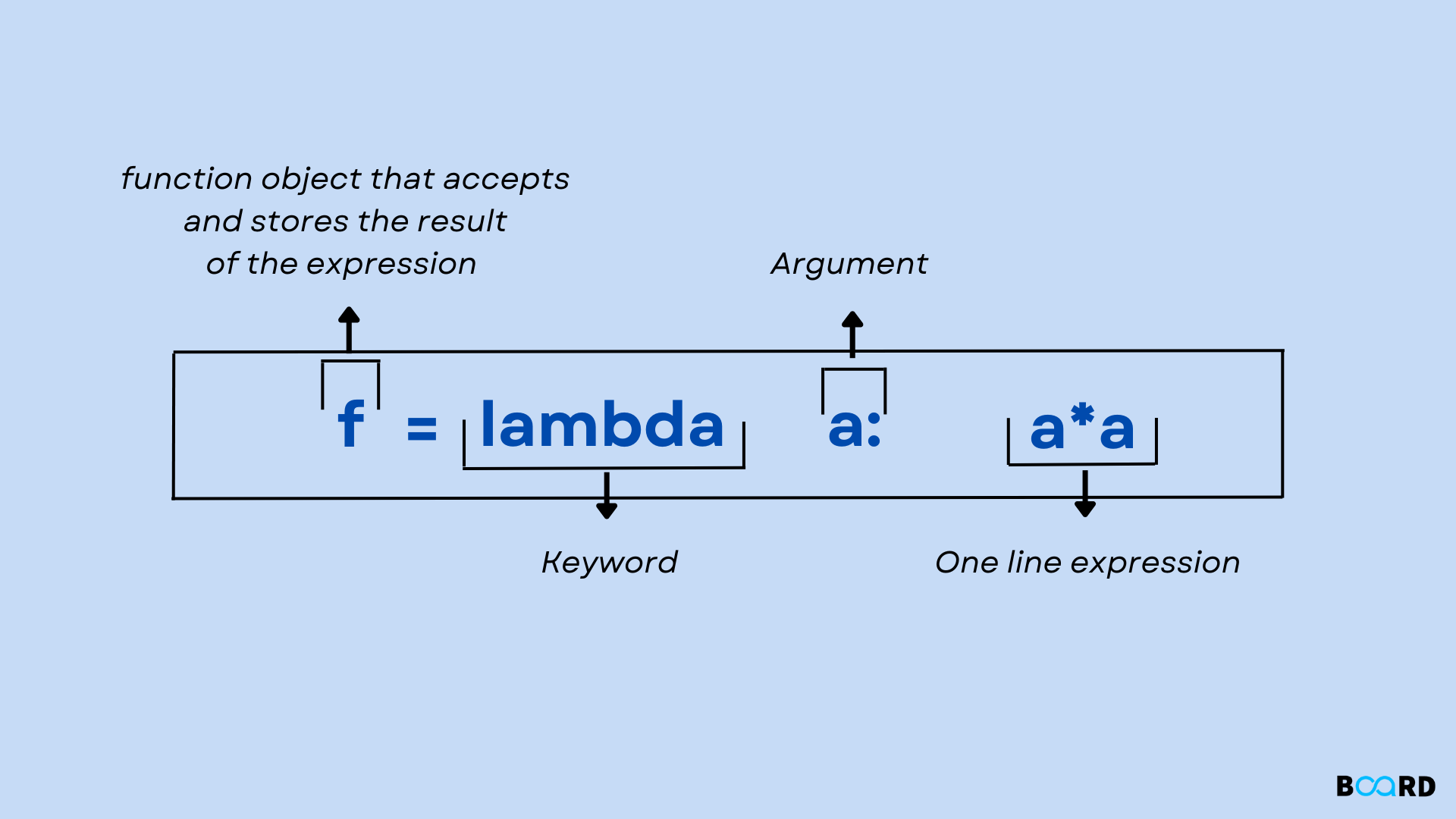
You can import specific functions or constants from the math module using the following syntax:

import math

print(math.pi)  # prints the value of pi (3.14159...)

Or, you can import the entire math module:

from math import *

print(pi)  # prints the value of pi (3.14159...)

This allows you to access the constants and functions using their original names.

For example, to calculate the sine of a number, you can use the following code:

import math

x = 45


sine_value = math.sin(math.radians(x))


print(f"The sine value of {x} degrees is {sine_value}")

In this example, we're using the math.radians() function to convert the angle from degrees to radians, and then calculating the sine using math.sin(). The output will be a numerical value representing the sine of 45 degrees.

When working with mathematical problems in Python, the math module provides an essential set of tools. It's crucial to understand the functions and constants available within this module to efficiently solve various mathematical problems.

Would you like me to elaborate on any specific aspect of the math module or provide examples for a particular problem?

Related Articles