dfs in python

dfs in python

I'm happy to respond in English and provide information on DFS (Depth-First Search) in Python.

What is Depth-First Search (DFS)?

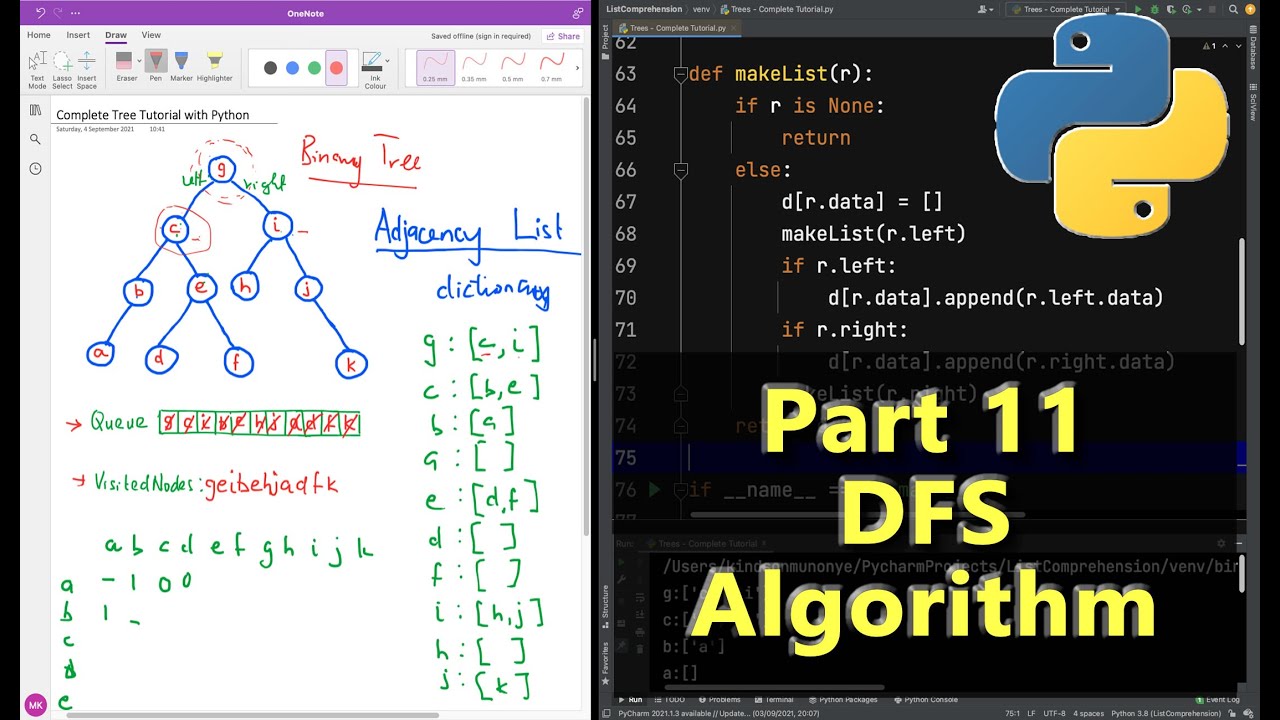
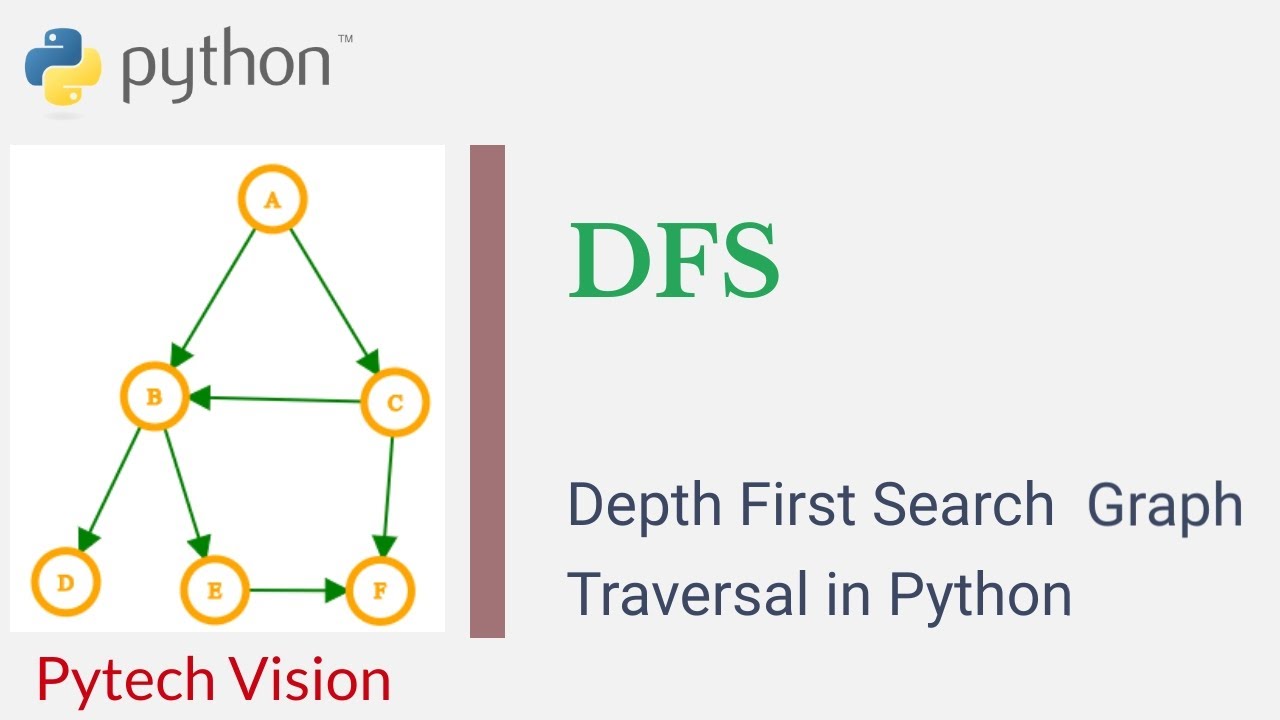
Depth-First Search (DFS) is a graph traversal algorithm that visits nodes in the order they are traversed, exploring as far as possible along each branch before backtracking. This approach is used to traverse or search tree-like or graph structures, such as decision trees or social networks.

How does DFS work?

The basic idea of DFS is to select an arbitrary node (the starting point) and then visit its neighbors, recursively traversing the graph until all reachable nodes have been visited.

Here's a step-by-step example:

Python Implementation:

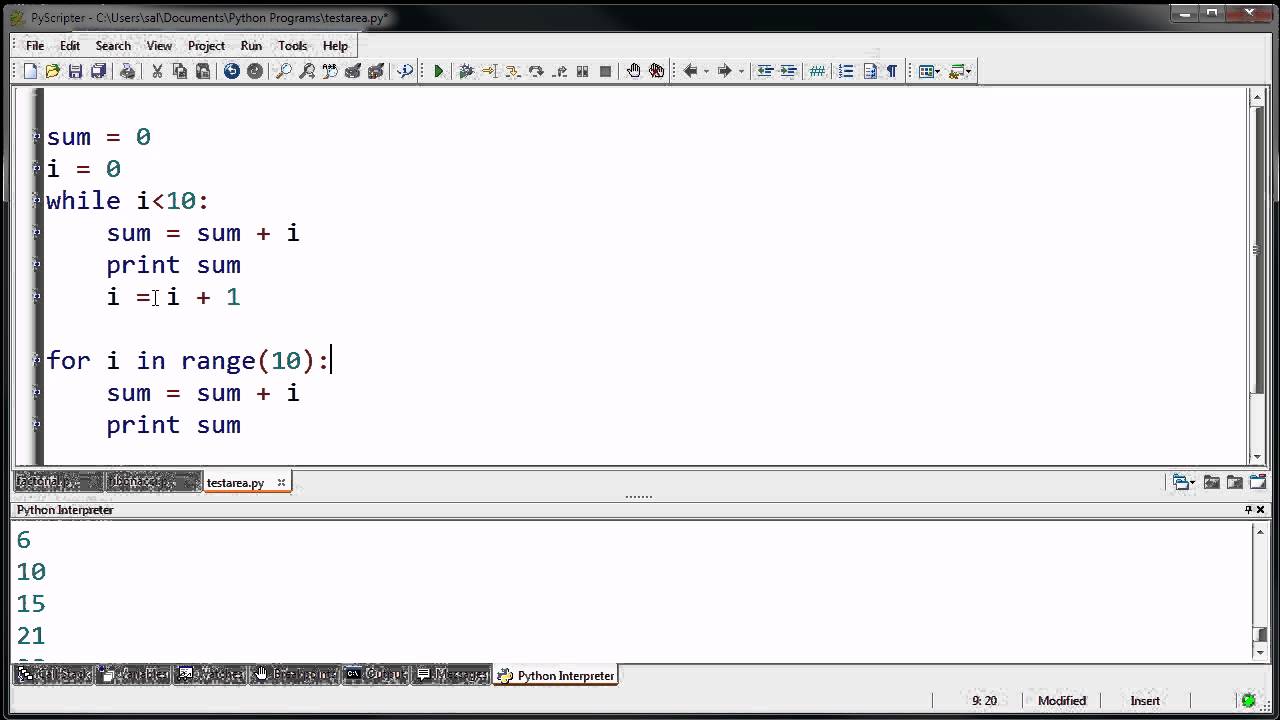
Here's a simple implementation of DFS in Python:

def dfs(graph, start):
visited = set()  # keep track of visited nodes
traversal_order = []  # store the order of visited nodes
def recursive_dfs(node):
visited.add(node)  # mark node as visited
traversal_order.append(node)  # add node to traversal order
for neighbor in graph[node]:
if neighbor not in visited:
recursive_dfs(neighbor)
recursive_dfs(start)
return traversal_order
Example usage:
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
start_node = 'A'
traversal_order = dfs(graph, start_node)
print(traversal_order)  # Output: ['A', 'B', 'D', 'E', 'F', 'C']

This implementation uses a recursive function recursive_dfs to traverse the graph starting from the given node. The dfs function returns a list of nodes in the order they were visited.

Time and Space Complexity:

The time complexity of DFS is O(|V| + |E|), where |V| is the number of vertices (nodes) and |E| is the number of edges in the graph.

The space complexity is O(|V|), as we need to store the visited nodes and traversal order.

I hope this helps you understand DFS and its implementation in Python!

What is the complexity of BFS in Python?

I'd be happy to explain the complexity of Breadth-First Search (BFS) in Python!

What is Breadth-First Search?

Before diving into its complexity, let's quickly review what BFS is. BFS is a graph traversal algorithm that explores all nodes at the current level before moving on to the next level. It's commonly used to find the shortest path between two nodes (also known as nodes) in an undirected graph or tree.

Complexity of BFS

The time complexity of BFS depends on several factors:

Time Complexity

The time complexity of BFS in Python (ignoring I/O operations) is generally O(E + V), where:

This is because BFS typically visits each edge once and each node at most twice (once to mark it as visited, and again to visit its neighbors). In the worst-case scenario, when all nodes have high degrees, the algorithm will spend more time processing these edges.

Space Complexity

The space complexity of BFS in Python, assuming a standard graph representation using an adjacency list or matrix, is generally O(V), where:

This is because we need to store visited nodes, which can grow up to V elements. In practice, you may not need to keep track of all visited nodes and only need a small buffer for storing temporary results.

Implementation in Python

In Python, the BFS algorithm typically involves:

Python's BFS implementation often leverages libraries like NetworkX or even a simple recursive function. You can find examples of Python code implementing BFS in various online resources, such as Stack Overflow or GitHub.

Conclusion

In conclusion, the complexity of BFS in Python depends on graph size and structure, with time complexity O(E + V) and space complexity O(V), assuming standard representations. Understanding these complexities is essential for choosing the most efficient algorithm for your specific use case.

I hope this explanation has been helpful! If you have any follow-up questions or need further clarification, please feel free to ask.