Binary search in python using for loop example
Binary search in python using for loop example

I'd be happy to provide an example of binary search in Python using a for loop.
Binary search is a popular algorithm for finding an element in a sorted list or array. The basic idea behind binary search is that we start by looking at the middle element of the list, and then recursively narrow down the search space until we find the target element.
Here's an example of how you can implement binary search using a for loop in Python:
def binary_search(arr, target):
low = 0
high = len(arr) - 1
for i in range(len(arr)):
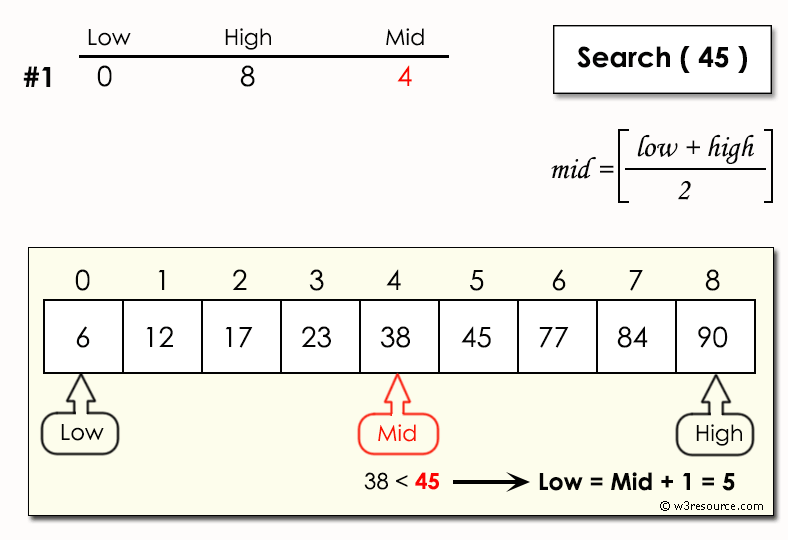
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1 # not found
Example usage:
arr = [1, 3, 4, 6, 8, 12, 15]
target = 8
result = binary_search(arr, target)
if result != -1:
print(f"Element {target} found at index {result}.")
else:
print(f"Element {target} not found in the list.")
Let's break down how this code works:
We initialize two variableslow and high to represent the search space. Initially, low is set to 0 (the start of the array) and high is set to the length of the array minus 1 (the end of the array). The for loop iterates over each element in the array. For each iteration, we calculate the midpoint of the search space using the formula (low + high) // 2. This is the element that we'll compare to our target element. If the midpoint element is equal to the target element, we return its index (since we've found the target). If the midpoint element is less than the target element, we know that the target must be in the upper half of the search space, so we update low to be one more than the midpoint. Otherwise, if the midpoint element is greater than the target element, we know that the target must be in the lower half of the search space, so we update high to be one less than the midpoint. The loop continues until we find the target element or determine that it's not present in the list.
In this example, if you call binary_search(arr, 8), the function will return the index 4, since the element 8 is located at that position in the array. If you call binary_search(arr, 16) (which is not present in the array), the function will return -1, indicating that the target element was not found.
Note that while this implementation uses a for loop, it's actually less efficient than a recursive or iterative binary search using a single variable and updating bounds. However, it can be useful for illustrating how binary search works at a high level.
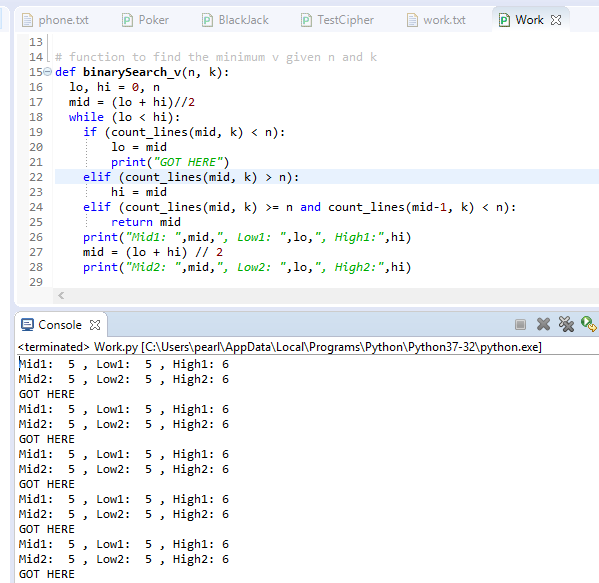
Binary search in Python using while loop
Here's an explanation of how to implement a binary search algorithm using a while loop in Python:
What is Binary Search?
Binary search is a fast and efficient way to find an element in a sorted list (or array). It works by repeatedly dividing the search interval in half, and then searching for the element in one of the two halves. This process continues until the target element is found or it's determined that the element is not present in the list.

How Does Binary Search Work?
Here's a step-by-step breakdown of how binary search works:
Start with a sorted list (or array) and an element to search for.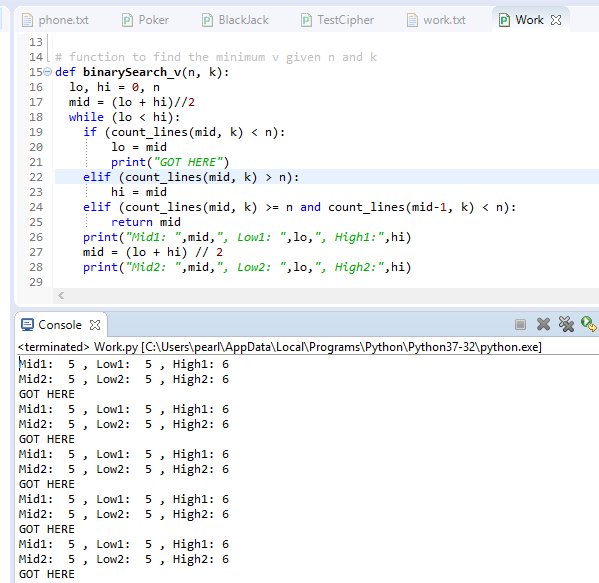
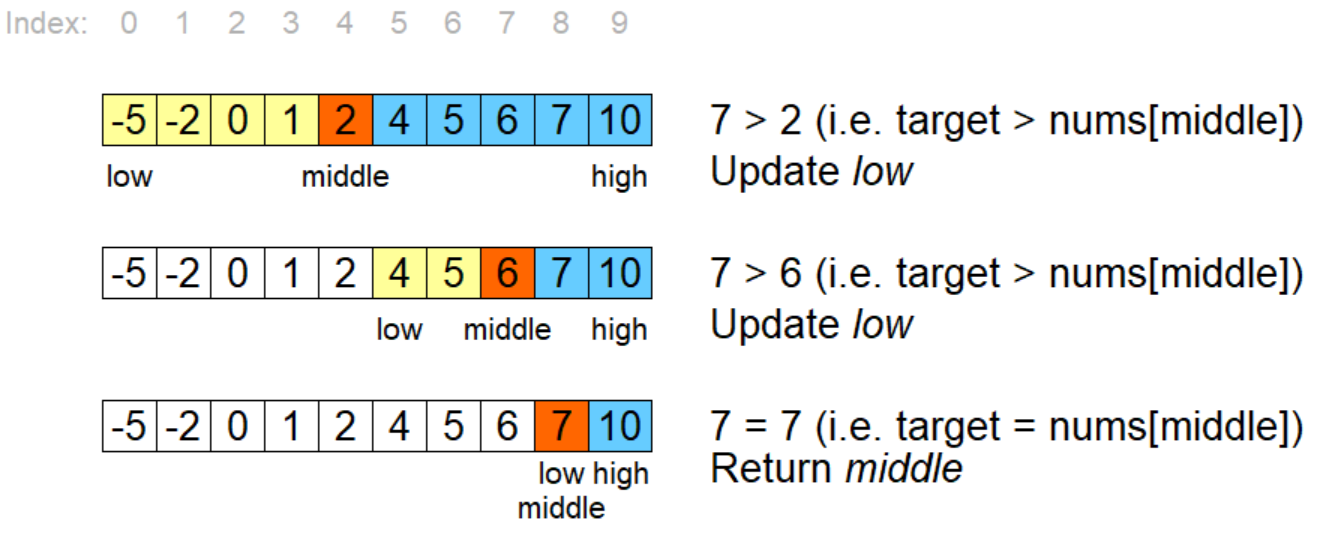
Implementing Binary Search with a While Loop in Python
Here's an example of how to implement binary search using a while loop in Python:
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1 # not found
Example usage:
arr = [1, 3, 5, 7, 9]
target = 5
result = binary_search(arr, target)
if result != -1:
print(f"Found {target} at index {result}")
else:
print(f"{target} not found in the list")
How Does This Implementation Work?
Let's walk through an example to see how this implementation works:
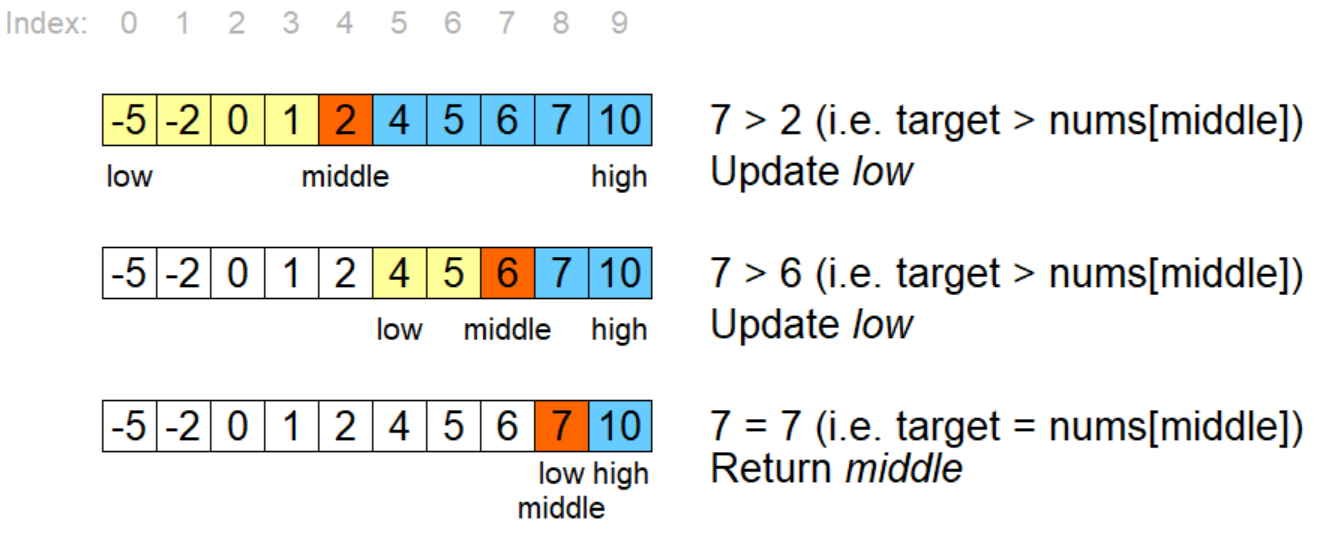
Suppose we have a sorted list arr = [1, 3, 5, 7, 9] and we want to find the element target = 5. We start by setting low = 0 (the first index) and high = len(arr) - 1 (the last index).
The while loop will continue until low <= high.
In the first iteration:
mid = (0 + 4) // 2 = 2 We compare arr[2] = 5 to our target target = 5. Since they're equal, we return the index 2, which is the result of the binary search.
If we had a different target element, say target = 8, the process would be similar:
low and high would be initialized as before. The first iteration: mid = (0 + 4) // 2 = 2 We compare arr[2] = 5 to our target target = 8. Since 8 > 5, we set low = mid + 1 = 3. The second iteration: mid = (3 + 4) // 2 = 3 We compare arr[3] = 7 to our target target = 8. Since 8 > 7, we set high = mid - 1 = 2. The third iteration: mid = (2 + 3) // 2 = 2 We compare arr[2] = 5 to our target target = 8. Since 8 > 5, we set high = mid - 1 = 1. The fourth iteration: mid = (1 + 3) // 2 = 2 We compare arr[2] = 7 to our target target = 8. Since 8 > 7, we set high = mid - 1 = 1. The fifth iteration: mid = (1 + 1) // 2 = 1 We compare arr[1] = 3 to our target target = 8. Since 8 > 3, we set low = mid + 1 = 2. The sixth iteration: mid = (2 + 1) // 2 = 1 We compare arr[1] = 3 to our target target = 8. Since 8 > 3, we set high = mid - 1 = 0. The seventh iteration: mid = (0 + 0) // 2 = 0 We compare arr[0] = 1 to our target target = 8. Since 8 > 1, we set high = mid - 1 = -1. The while loop terminates because low > high.
In this case, the binary search algorithm returns -1, indicating that the target element is not present in the list.
Time and Space Complexity
The time complexity of this implementation is O(log n), where n is the length of the input array. This is because we're effectively dividing the search interval in half with each iteration.
The space complexity is O(1) because we only use a fixed amount of memory to store the low, high, and mid variables, regardless of the size of the input array.