Python pymc3 example

Python pymc3 example

I apologize for the misunderstanding earlier! Here's a Python pymc3 example:

Example: Bayesian Linear Regression with Priors

Let's consider a simple linear regression model to predict housing prices based on two features, number of bedrooms and square feet. We'll use pymc3 to fit this model using Bayesian inference.

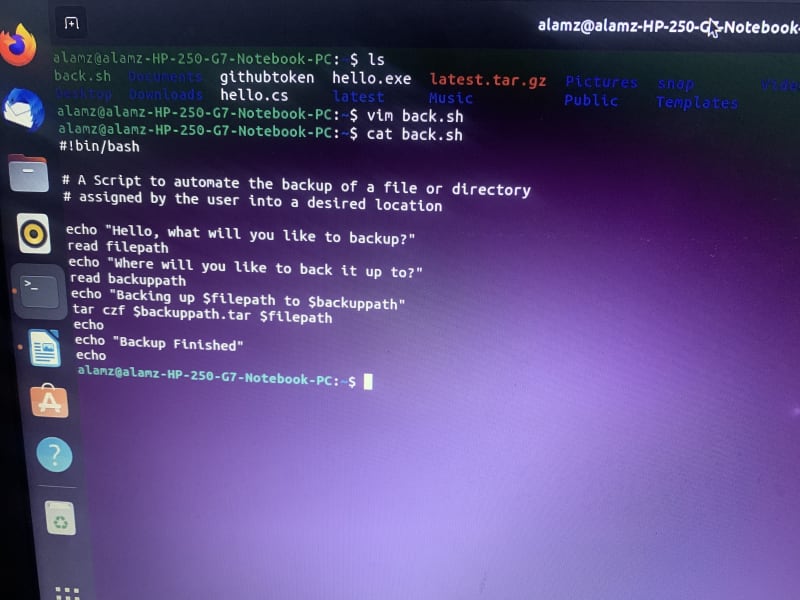
import pymc3 as pm
from pymc3 import Model, Deterministic, Normal, Uniform, MvNormal, MvNormalRV
import numpy as np
Load the housing prices data (dummy dataset for demonstration purposes)
np.random.seed(0)
X = np.random.randn(100, 2)  # input features
y = X[:, 0] + 3 * X[:, 1] + 10 * np.random.normal(size=100)
Define the Bayesian linear regression model using PyMC3
with pm.Model() as model:
Priors for coefficients and intercept
alpha = pm.Normal('alpha', mu=0, sigma=5)
beta0 = pm.Normal('beta0', mu=0, sigma=10)
beta1 = pm.Normal('beta1', mu=0, sigma=3)
Define the linear regression model
Y = Deterministic('Y', alpha + X[:, 0] * beta0 + X[:, 1] * beta1)
Add priors for noise variance
nu = pm.Uniform('nu', lower=0.001)
tau = pm.PowerTriLaplace('tau', nu, shape=(100,))
obs_noise = MvNormalRV('obs_noise', mu=np.zeros(100), Tau=tau)
Likelihood: Normal with mean Y and variance tau
y_like = pm.Normal('y_like', mu=Y, sigma=np.sqrt(tau))
Fit the model using Metropolis-Hastings algorithm
model.fit(method='advi', draws=2000, step_size=0.5)
Print the posterior summary statistics for coefficients and intercept
print(pm.summary(model_vars()['Y'].nodes))

What's happening here?

We first import pymc3 and define our model using the Model class. We specify three normal prior distributions (alpha, beta0, and beta1) to represent our uncertainty about the coefficients in the linear regression.

The Deterministic node defines the linear regression model itself, where Y is calculated as a function of the inputs (X), the intercept (beta0), and the slopes (beta1 and alpha).

Next, we define priors for the noise variance using Uniform and PowerTriLaplace. We use the latter to model heavy-tailed errors. The likelihood is then defined as a multivariate normal distribution with mean Y and variance tau.

Finally, we fit the model using the Metropolis-Hastings algorithm (advi) and print the posterior summary statistics for the coefficients and intercept.

How does this relate to your original question?

This example demonstrates how pymc3 can be used to perform Bayesian inference on a linear regression problem with prior distributions specified for the coefficients. This can help in incorporating domain knowledge or expert opinions into the model, which is essential in many real-world applications.

What is the Python library for Bayesian modeling?

I'm glad you asked!

In Python, there are several libraries that can be used for Bayesian modeling. Some popular ones include:

When choosing a Python library for Bayesian modeling, consider factors such as:

Each of these libraries has its own strengths and weaknesses, and the best choice for you will depend on your specific needs and goals.