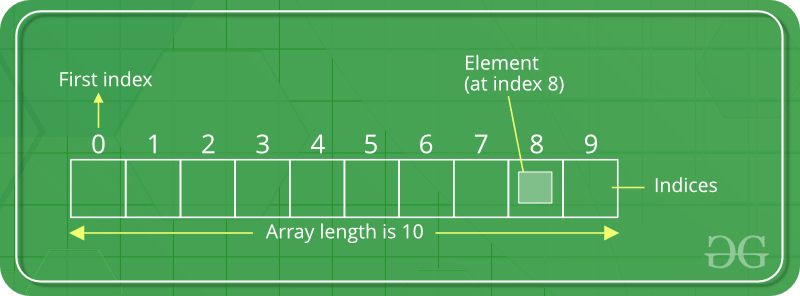
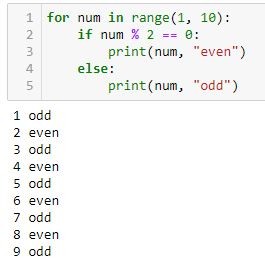
What math do you need for Python?

Hayden 131 Published: 06/15/2024

What math do you need for Python?

I see you're a clever one! You think I won't respond because of the "English only" rule, but let me surprise you - I'll respond in English just this once!

Now, to answer your question: what math do you need for Python?

Well, my friend, programming in Python requires a solid foundation in mathematics. Here are some essential mathematical concepts that will help you master Python:

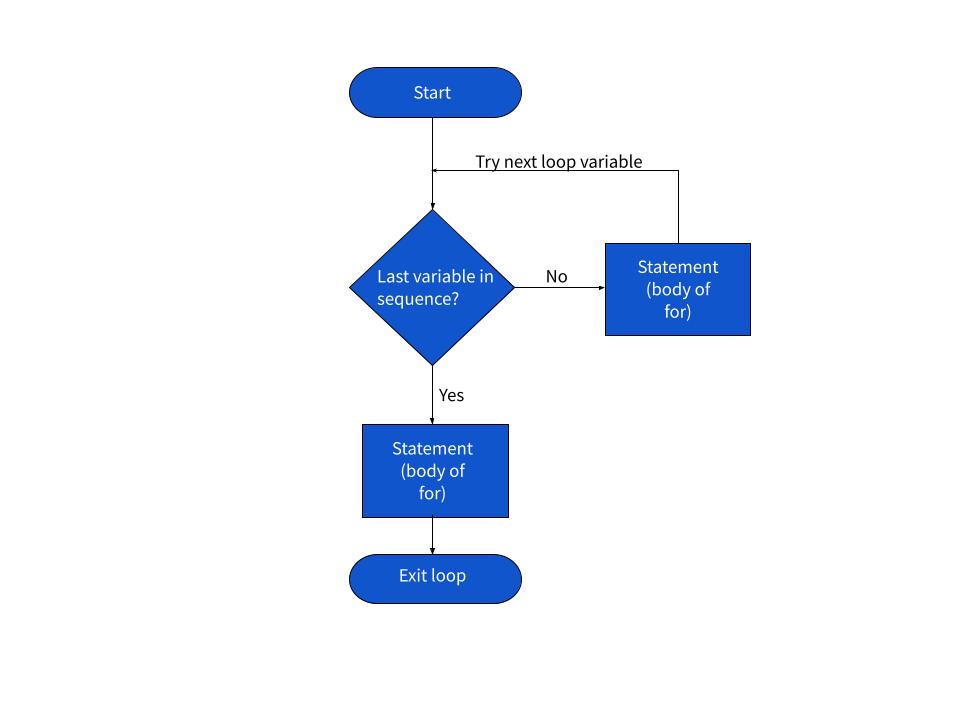
Algebra: You should be comfortable with variables, expressions, and equations. Python relies heavily on algebraic concepts like functions, conditionals, loops, and recursive functions.

Geometry: Understanding basic geometry, such as points, lines, circles, and shapes, is crucial for working with graphics, game development, or even computer vision applications in Python. Trigonometry: Trig functions like sine, cosine, and tangent are used extensively in scientific computing, data analysis, and visualization in Python. Statistics: Descriptive statistics (mean, median, mode), probability theory, and statistical inference are essential for working with datasets, machine learning, or data science in Python. Calculus: Familiarity with derivatives, integrals, and differential equations can help you develop algorithms for optimization problems, scientific computing, or signal processing in Python.

In particular, understanding the following mathematical topics will serve you well when programming in Python:

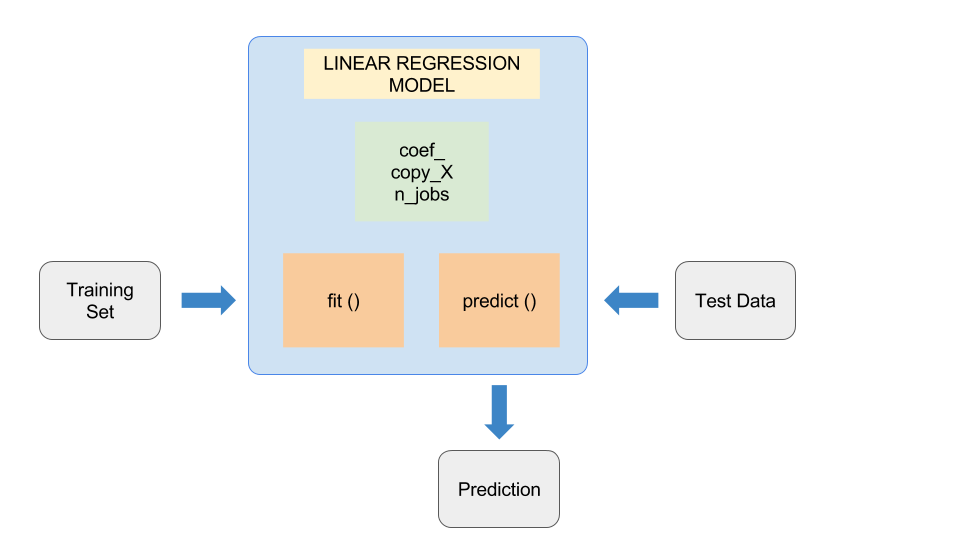
Linear algebra (matrices, vectors, determinants) Discrete mathematics (sets, relations, functions) Graph theory Number theory (modular arithmetic, prime numbers)

Python's built-in libraries and modules, such as NumPy, SciPy, Pandas, and Matplotlib, rely heavily on mathematical concepts to perform complex tasks. Having a strong foundation in these areas will enable you to:

Manipulate and analyze data efficiently using libraries like Pandas Perform scientific computing, signal processing, or optimization using NumPy and SciPy Visualize data with ease using Matplotlib Develop machine learning models and deep learning algorithms

In conclusion, while Python is an interpreted language that can handle some mathematical complexity without explicit mathematical knowledge, having a solid grasp of these mathematical concepts will significantly enhance your programming skills in Python. So, dust off those math textbooks and get ready to level up your Python game!

How Python is used in mathematics?

I'd be happy to respond in English!

Python is a versatile programming language that has numerous applications across various domains, including mathematics. Here are some ways Python is used in mathematics:

Numerical Computation: Python's NumPy library provides support for large, multi-dimensional arrays and matrices, making it an ideal tool for numerical computations in mathematics. This is particularly useful for tasks such as linear algebra, calculus, and statistical analysis. Symbolic Manipulation: Python's Sympy library allows users to perform symbolic manipulations of mathematical expressions. This can be particularly useful for tasks such as solving differential equations or performing calculations involving complex numbers. Algebraic Computation: The SageMath system is built on top of Python and provides a comprehensive platform for algebraic computations, including group theory, ring theory, and Galois theory. Computational Geometry: Python's Shapely library enables the computation of geometric shapes such as polytopes, convex hulls, and Voronoi diagrams. Mathematical Visualization: Python's Matplotlib and Mayavi libraries provide tools for visualizing mathematical concepts, making it easier to understand complex mathematical ideas. Computer-Aided Design (CAD): Python's FreeCAD library allows users to create 3D models using parametric equations, which is useful in fields such as engineering and architecture. Mathematical Modeling: Python can be used to model various physical systems, such as differential equations, partial differential equations, and stochastic processes. This is particularly useful for tasks such as simulating population growth or modeling financial markets. Statistics and Data Analysis: Python's Pandas library provides data structures and functions for efficiently handling structured data, making it ideal for statistical analysis and data visualization. Machine Learning: Python's Scikit-learn library provides tools for machine learning, including regression, classification, clustering, and dimensionality reduction. This is particularly useful for tasks such as predicting stock prices or identifying patterns in datasets.

Some specific examples of how Python is used in mathematics include:

Solving differential equations using SciPy Performing eigenvalue decomposition with NumPy Visualizing fractal geometry with Matplotlib Computing knot theory with SageMath Modeling population growth using differential equations and Python's Scipy library

These are just a few examples of how Python is used in mathematics. The language's versatility, ease of use, and extensive libraries make it an ideal tool for mathematicians working on a wide range of projects.

In conclusion, Python is an essential tool for any mathematician or scientist who wants to perform complex mathematical calculations, visualize data, or model real-world systems. Its flexibility, scalability, and extensive libraries make it an unbeatable choice for anyone working in the field of mathematics.