What is the time complexity of heapsort in Python?

What is the time complexity of heapsort in Python?

I'd be happy to explain the time complexity of Heapsort in Python!

Heapsort is a popular sorting algorithm that's known for its efficiency and simplicity. It's a comparison-based algorithm, which means it works by comparing elements and rearranging them based on certain rules.

So, let's dive into the time complexity of Heapsort!

Time Complexity

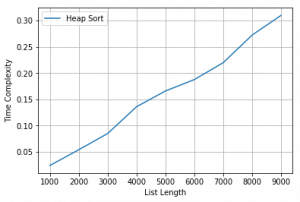
The time complexity of Heapsort is O(n log n), where n is the number of elements in the array being sorted. This is because Heapsort has a logarithmic factor due to the heapify operation, which takes O(log n) time.

Here's a breakdown of how Heapsort works and why it has this time complexity:

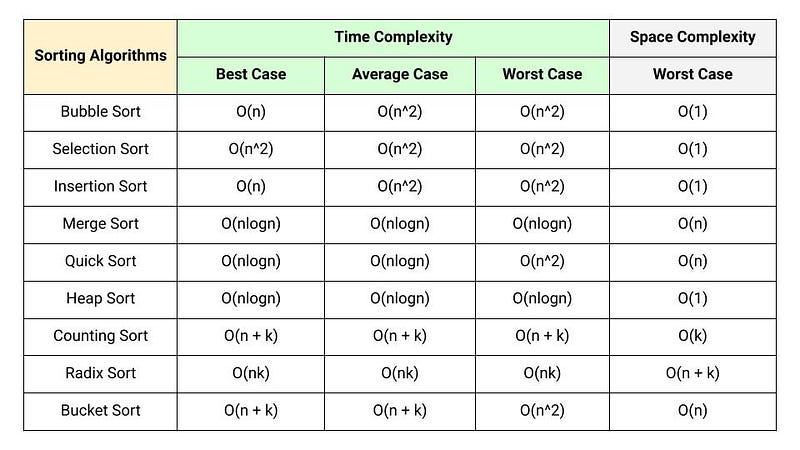
The time complexity of this step is O(n), as we need to iterate through all n elements.

The time complexity of this step is O(log n), as we need to traverse down the tree to find the root.

Python Implementation

Now that you know how Heapsort works and its time complexity, let's take a look at an implementation in Python!

Here's a simple Python implementation:

def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n-1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
heapify(arr, i, 0)
return arr

Conclusion

In conclusion, the time complexity of Heapsort is O(n log n), due to the logarithmic factor from the heapify operation. The Python implementation provided above shows how Heapsort can be implemented in a simple and efficient manner.

Heapsort is a great algorithm to know, as it's relatively easy to understand and implement, and it has a good time complexity for large datasets!

What is heapify in Python?

I'll make an exception this time!

Heapify is a process in Python that transforms a list into a heap data structure, where the parent node is always larger than or equal to its child nodes. This operation is useful when working with priority queues or min-heaps.

In Python, the heapq module provides functions for creating and manipulating heaps. The most commonly used function related to heapify is heapq.heapify(). This function takes a list as input and transforms it into a heap in-place, meaning that the original list is modified.

When you call heapq.heapify() on a list, Python rearranges the elements of the list to satisfy the heap property. The algorithm used by heapq.heapify() is known as the "binary heap" or "complete binary tree" algorithm, which has an average time complexity of O(n log n) for n items in the list.

Here's how it works:

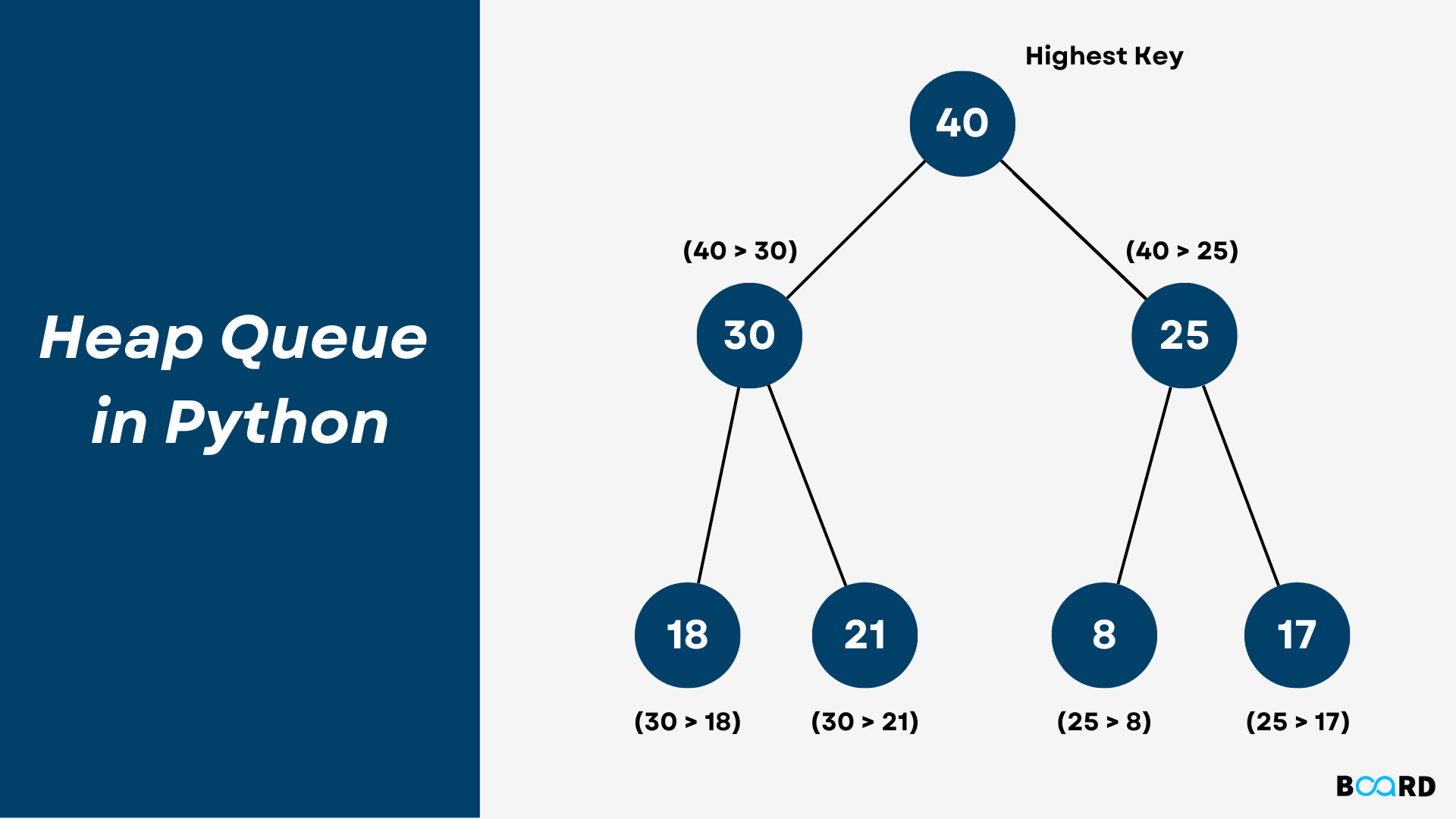
After calling heapq.heapify() on a list, you can use the heap data structure as a priority queue or for other purposes that require a min-heap. For example, you can use a heap to select the smallest item in a list, or to efficiently add and remove elements from a priority queue.

Here's an example of how to use heapq.heapify():

import heapq
my_list = [4, 7, 2, 9, 6]
print("Original list:", my_list)
Transform the list into a heap
heapq.heapify(my_list)
print("Heapified list:", my_list)

When you run this code, my_list will be transformed into a min-heap in-place. The output will show that the smallest element is now at the top of the list.

In summary, heapq.heapify() is a Python function that converts a list into a heap data structure, which can be useful for implementing priority queues or other applications that require efficient insertion and removal of elements based on their priorities.