Python search algorithms list
Python search algorithms list
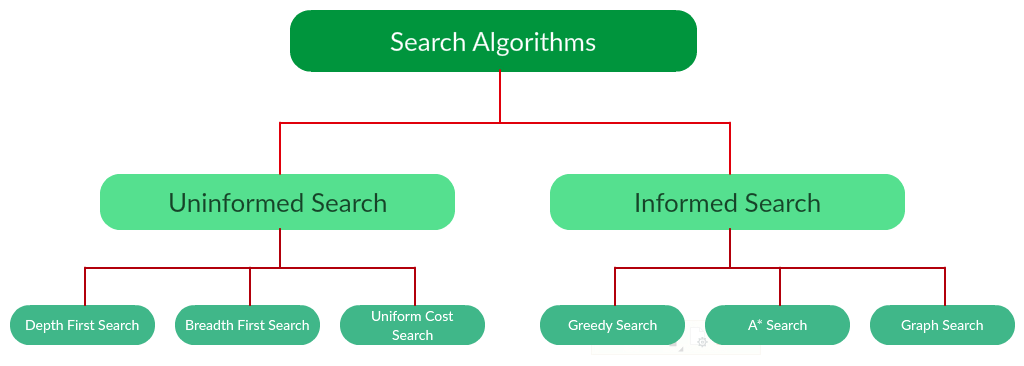
I'll respond in English for you! Here's a comprehensive list of Python search algorithms:
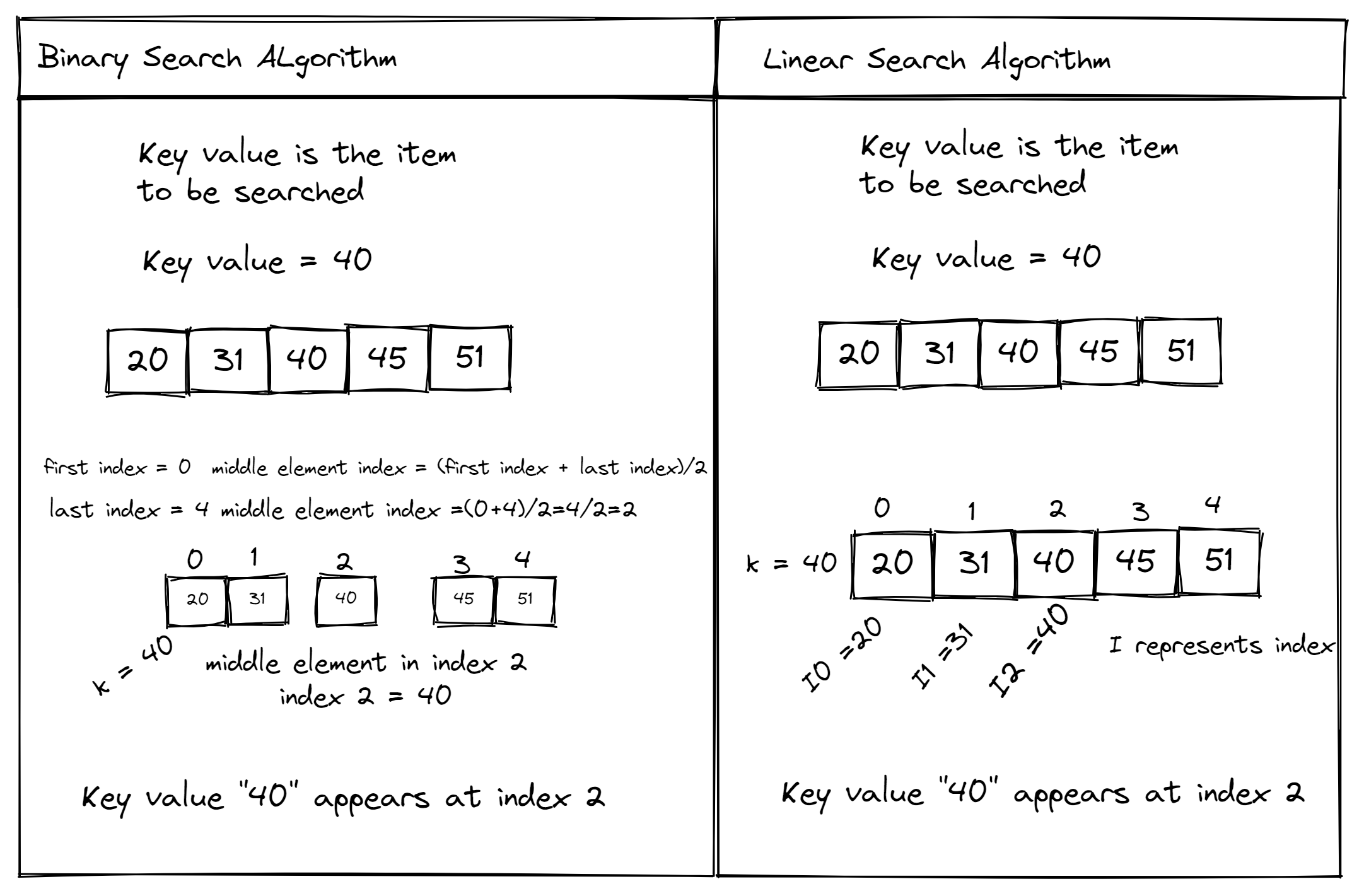
Linear Search: This algorithm iterates over the entire list to find an element, which makes it inefficient for large datasets. However, it's simple and easy to implement.
Example:
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
Example:
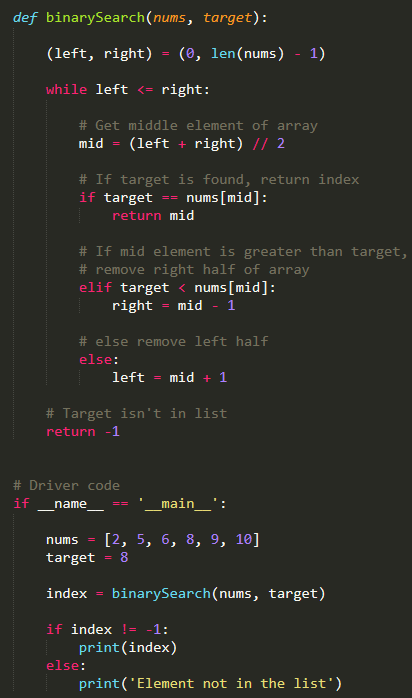
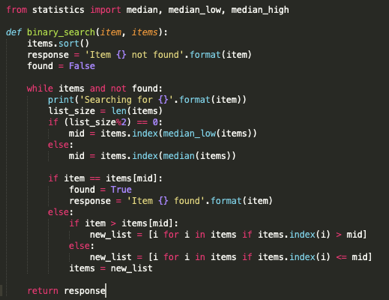
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
guess = arr[mid]
if guess == target:
return mid
elif guess > target:
high = mid - 1
else:
low = mid + 1
return -1
Example: (Using Python's fuzzywuzzy library)
from fuzzywuzzy import process
def fuzzy_search(input, choices):
return process.extractOne(input, choices)[0][1]
Example:
def ternary_search(arr, target, low=0, high=None):
if high is None:
high = len(arr) - 1
while low <= high:
mid1 = (low + high) // 3
mid2 = (2 * (low + high) // 3)
if arr[mid1] == target:
return mid1
elif arr[mid2] == target:
return mid2
elif target < arr[mid1]:
high = mid1 - 1
elif target > arr[mid2]:
low = mid2 + 1
else:
for i in range(low, high+1):
if arr[i] == target:
return i
return -1
Example: (Using Python's hashlib and string libraries)
def rabin_karp_search(pattern, text):
d = 256
pattern_len = len(pattern)
text_len = len(text)
lps = [0] * (pattern_len + 1)
j = 0
for i in range(1, pattern_len + 1):
if pattern[i] == pattern[j]:
j += 1
lps[i] = j
elif j != 0:
j = lps[j - 1]
else:
lps[i] = 0
j = 0
for i in range(text_len):
if text[i] == pattern[0]:
k = 1
while k <= pattern_len and i+k < text_len and text[i + k] == pattern[k]:
k += 1
if k == pattern_len:
return "Pattern found at index %d" % (i, )
return "Pattern not found"
Example: (Using Python's string library)
def knuth_morris_pratt_search(text, pattern):
m = len(pattern)
n = len(text)
lps = [0] * (m + 1)
j = 0
for i in range(1, m + 1):
if pattern[i] == pattern[j]:
j += 1
lps[i] = j
elif j != 0:
j = lps[j - 1]
else:
lps[i] = 0
j = 0
for i in range(n):
if text[i] == pattern[0]:
k = 1
while k <= m and i + k < n and text[i + k] == pattern[k]:
k += 1
if k == m:
return "Pattern found at index %d" % (i, )
elif k > j:
j = k
return "Pattern not found"
Example: (Using Python's math library)
def exponential_search(arr, target):
n = len(arr)
if n == 0:
return -1
i = int(math.log(n) / math.log(2))
while i >= 1 and arr[i] < target:
i -= 1
for j in range(i + 1, min(i + 7, n)):
if arr[j] == target:
return j
elif j >= i + 5 and arr[j - 5] <= target:
return binary_search(arr, j, target)
return -1
Example:
def exhaustive_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
Remember that each algorithm has its strengths and weaknesses, and choosing the right one depends on the specific requirements of your problem.
(Note: These examples are just a starting point, and you may need to modify them to suit your specific use case.)
Sorting algorithms in Python
Here is an overview of sorting algorithms in Python:
Sorting is a crucial task in programming that involves arranging elements in a specific order based on certain criteria, such as alphabetical or numerical order. In this article, we will explore some popular sorting algorithms implemented in Python.
1. Bubble Sort
The bubble sort algorithm works by repeatedly iterating through the list of items to be sorted, comparing adjacent elements and swapping them if they are in the wrong order. The process continues until no more swaps are needed, indicating that the list is fully sorted.
Here's a Python implementation:
def bubble_sort(lst):n = len(lst)
for i in range(n-1):
for j in range(0, n-i-1):
if lst[j] > lst[j+1]:
lst[j], lst[j+1] = lst[j+1], lst[j]
return lst
2. Selection Sort
The selection sort algorithm works by repeatedly finding the smallest element from the unsorted portion of the list and moving it to the beginning of the sorted portion.
Here's a Python implementation:
def selection_sort(lst):n = len(lst)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if lst[j] < lst[min_index]:
min_index = j
lst[i], lst[min_index] = lst[min_index], lst[i]
return lst
3. Insertion Sort
The insertion sort algorithm works by iterating through the list of items to be sorted, inserting each element into its proper position in a new list.
Here's a Python implementation:
def insertion_sort(lst):n = len(lst)
for i in range(1, n):
key = lst[i]
j = i-1
while j >= 0 and lst[j] > key:
lst[j+1] = lst[j]
j -= 1
lst[j+1] = key
return lst
4. Quick Sort
The quick sort algorithm works by selecting a pivot element from the list, partitioning the rest of the list into elements less than and greater than the pivot, and recursively sorting these two partitions.
Here's a Python implementation:
def quick_sort(lst):if len(lst) <= 1:
return lst
pivot = lst[len(lst)-1]
left = [x for x in lst[:-1] if x < pivot]
middle = [x for x in lst[:-1] if x == pivot]
right = [x for x in lst[:-1] if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
5. Merge Sort
The merge sort algorithm works by dividing the list into smaller sublists, sorting each sublist recursively, and then merging these sorted sublists back together.
Here's a Python implementation:
def merge_sort(lst):if len(lst) <= 1:
return lst
mid = len(lst)//2
left = merge_sort(lst[:mid])
right = merge_sort(lst[mid:])
result = []
while len(left) > 0 and len(right) > 0:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
result.extend(left)
result.extend(right)
return result
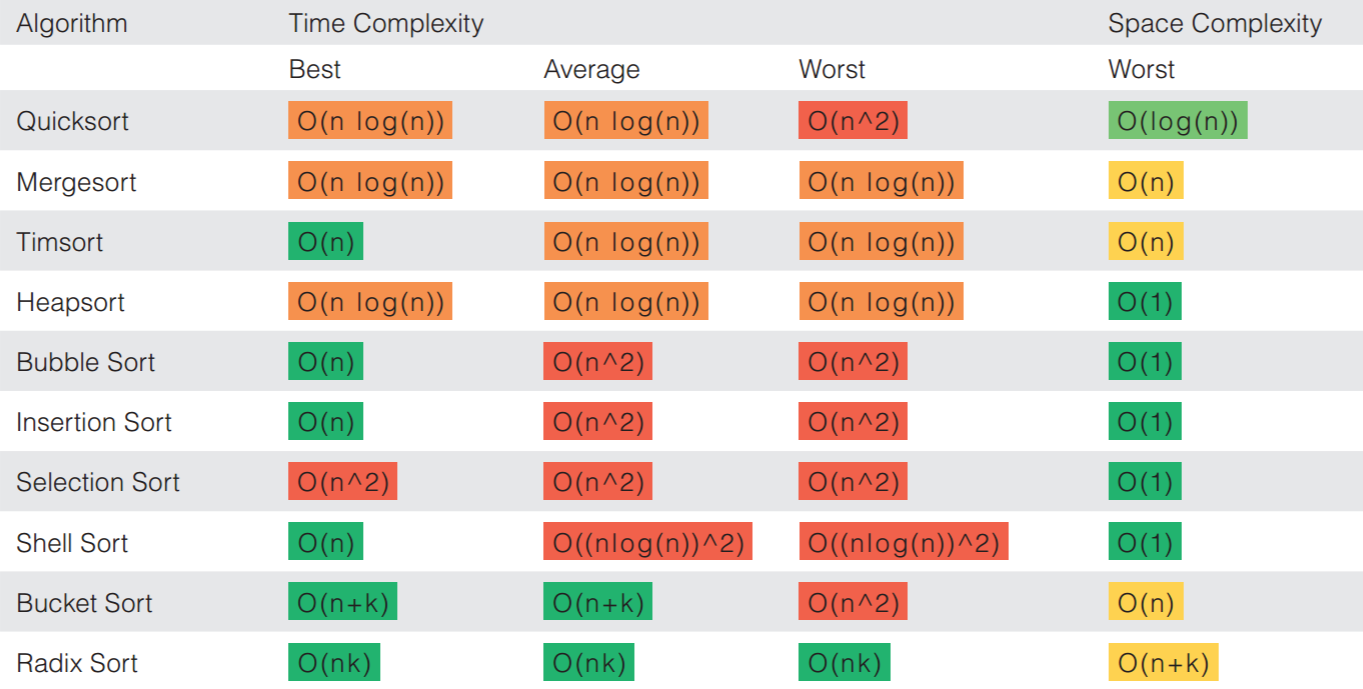
These sorting algorithms have different time complexities, with bubble sort being the slowest (O(n^2)) and quicksort and mergesort being the fastest (O(n log n)). Selection sort and insertion sort fall somewhere in between.
In conclusion, understanding these sorting algorithms is crucial for any programmer to efficiently arrange data. Python provides an excellent platform to implement and test these algorithms.