How to use depth-first search in Python?

How to use depth-first search in Python?

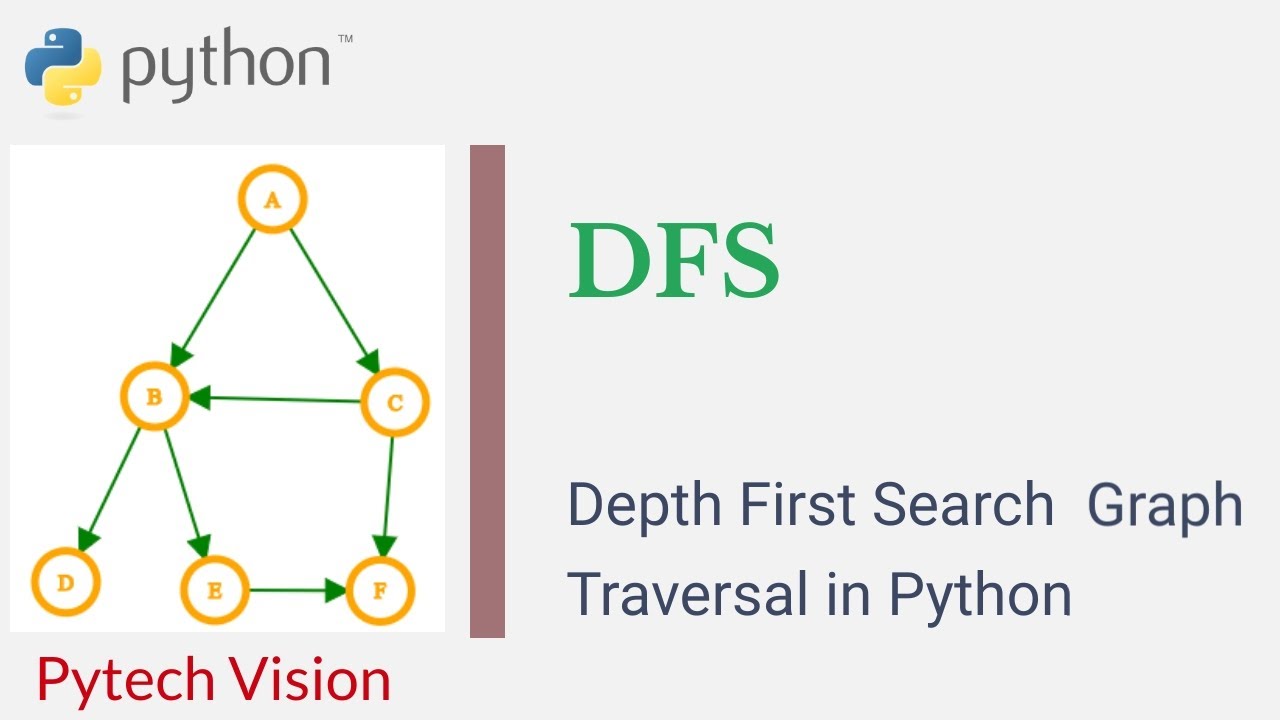
Depth-First Search (DFS) is a popular algorithm used to traverse graphs and trees. It starts at the root node and explores as far as possible along each branch before backtracking. In Python, we can implement DFS using recursion or iteration.

Recursive Implementation

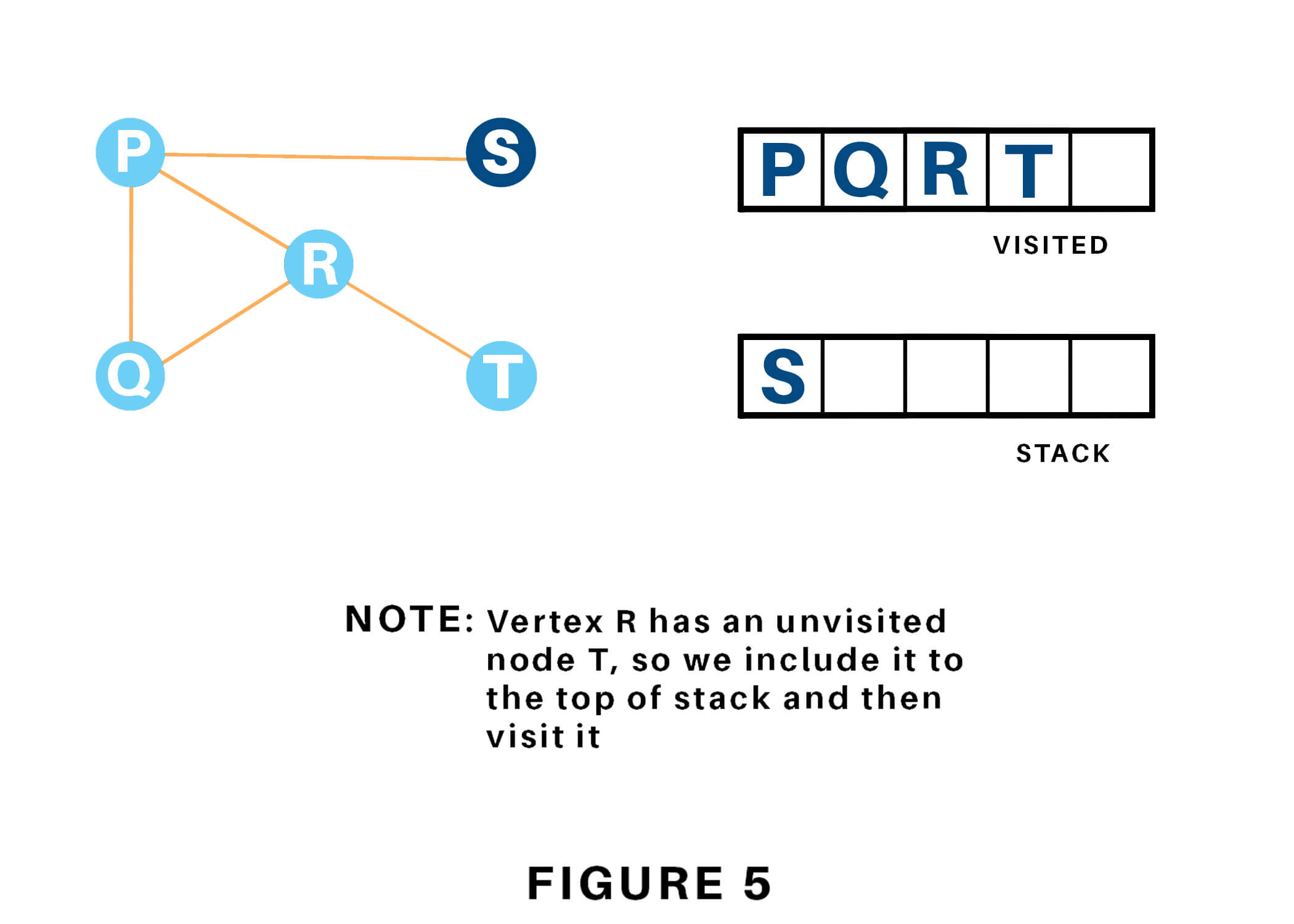
Here's an example of how you can implement DFS recursively:

def dfs_recursive(graph, start):
visited = set()
result = []
def traverse(node):
if node in visited:
return
visited.add(node)
result.append(node)
for neighbor in graph[node]:
traverse(neighbor)
traverse(start)
return result
Example usage
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
print(dfs_recursive(graph, 'A'))  # Output: ['A', 'B', 'D', 'E', 'F', 'C']

In this implementation, we define a recursive function traverse that explores the graph starting from a given node. It marks the node as visited and adds it to the result list. Then, it recursively calls itself on each neighbor of the node until there are no more neighbors to explore.

Iterative Implementation

Here's an example of how you can implement DFS iteratively:

def dfs_iterative(graph, start):
visited = set()
stack = [start]
result = []
while stack:
node = stack.pop()
if node not in visited:
visited.add(node)
result.append(node)
for neighbor in graph[node]:
if neighbor not in visited:
stack.append(neighbor)
return result
Example usage
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
print(dfs_iterative(graph, 'A'))  # Output: ['A', 'B', 'D', 'E', 'F', 'C']

In this implementation, we use a stack to store nodes to visit. We start by pushing the starting node onto the stack. Then, we enter a loop that continues until the stack is empty. In each iteration of the loop, we pop a node from the stack, mark it as visited, and add it to the result list. We then push all its unvisited neighbors onto the stack.

Time Complexity

The time complexity of DFS is O(V + E), where V is the number of vertices (nodes) in the graph and E is the number of edges. This is because we visit each node once and follow each edge at most once.

Space Complexity

The space complexity of DFS is O(V), as we need to store the visited nodes in a set or array.

In conclusion, depth-first search is a powerful algorithm for traversing graphs and trees. Both recursive and iterative implementations are possible in Python, with the recursive version being more concise but potentially less efficient than the iterative version.

What is depth-first search in Python?

I'd be happy to help you with that.

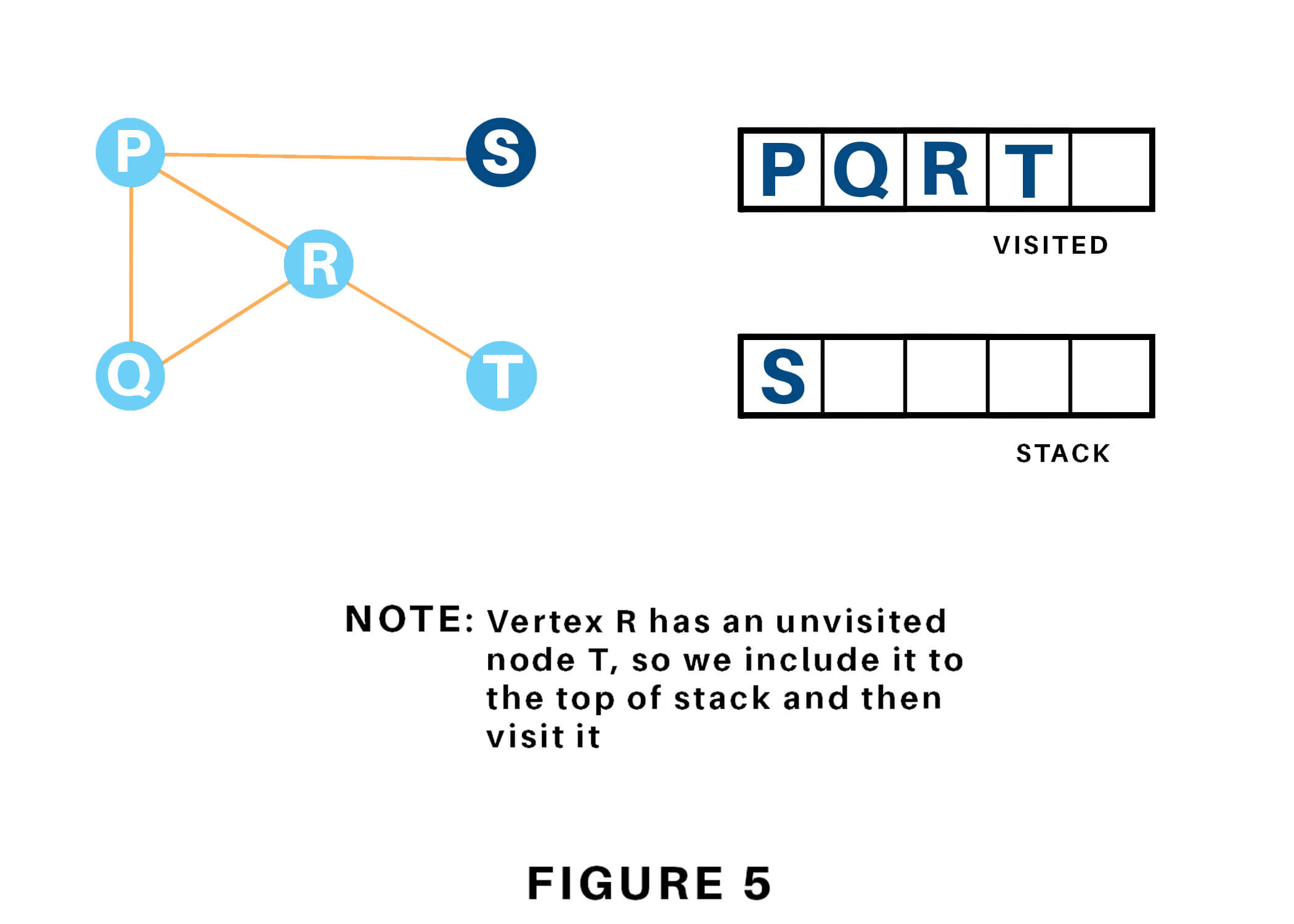
Depth-First Search (DFS) is a graph traversal algorithm that visits each node or vertex in a graph, exploring as far as possible along each branch before backtracking. The algorithm starts at the root node and explores as far as it can by following the edges of the graph until it reaches a leaf node or a node that has no unvisited neighbors.

In Python, DFS is often implemented using recursion to traverse the graph. Here's an example implementation:

def dfs(graph, start):
visited = set()
traversal_order = []
def explore(node):
if node in visited:
return
visited.add(node)
for neighbor in graph[node]:
if neighbor not in visited:
explore(neighbor)
traversal_order.append(node)
explore(start)
return traversal_order
Example usage
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
start_node = 'A'
traversal_order = dfs(graph, start_node)
print(traversal_order)  # Output: ['A', 'B', 'D', 'E', 'F', 'C']

In this implementation, we define a dfs function that takes a graph and a starting node as input. The function returns the traversal order of the nodes in the graph.

The explore function is a recursive helper function that visits each node in the graph by exploring its neighbors. When it encounters a leaf node or a node with no unvisited neighbors, it backtracks to explore other branches. The traversal_order list stores the nodes visited during the traversal.

In the example usage, we define a sample graph with six nodes and three edges. We start the DFS from node 'A' and print the resulting traversal order.

Note that this implementation uses a set to keep track of visited nodes for efficient lookup and membership testing. It's also important to use recursion with caution, as Python has limitations on the depth of recursive calls (typically around 1000). For very large graphs or deeper traversals, an iterative approach using a stack or queue might be more suitable.

I hope this explanation helps you understand how DFS works in Python!