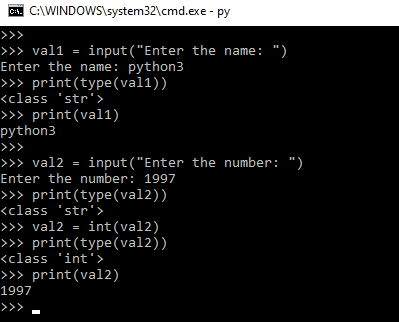
What is the mean of input in python with example

What is the mean of input in python with example

I'm happy to help!

What is the mean?

In mathematics, the mean (also known as average) is a measure of the central tendency of a set of numbers or values. It's one way to summarize a dataset by finding a value that represents the "typical" or "average" value in the data.

What is the mean function in Python?

Python provides a built-in statistics module that includes various functions for calculating statistical measures, including the mean (also known as average). The mean() function takes an iterable (like a list or tuple) as input and returns the mean value of the numbers in the iterable.

Example: Calculating Mean using Python

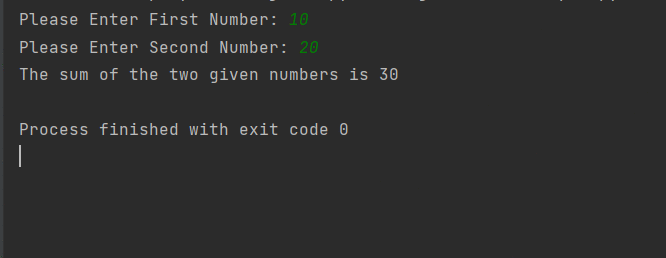
Here's an example to calculate the mean of some numbers:

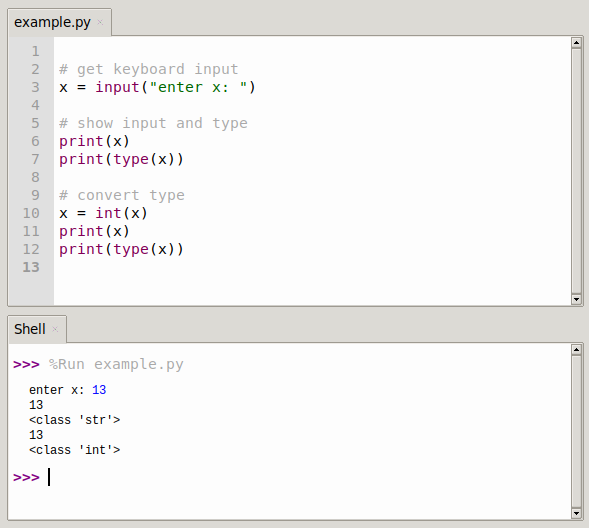
import statistics
numbers = [1, 2, 3, 4, 5]
mean_value = statistics.mean(numbers)
print(f"The mean of {numbers} is: {mean_value}")

When you run this code, it will output:

The mean of [1, 2, 3, 4, 5] is: 3.0

As expected, the mean value is 3, which is the average of the numbers in the list.

How does statistics.mean() work?

Underneath the hood, statistics.mean() calculates the sum of all values and then divides it by the number of elements in the iterable. Here's a step-by-step breakdown:

In our example, the sum is 15 (1 + 2 + 3 + 4 + 5), and there are 5 elements in the list. So, (15) / 5 = 3.

Conclusion

The statistics.mean() function in Python provides a convenient way to calculate the mean of a dataset. With this function, you can easily find the average value of a set of numbers, making it a useful tool for data analysis and visualization.

Now that you know how to calculate the mean using Python, go ahead and explore more statistical functions and concepts!

What is mean in Python?

I'd be happy to explain what "mean" means in the context of Python programming.

In general, the term "mean" refers to an average value calculated from a set of numbers or values. In mathematics and statistics, there are several ways to calculate the mean of a set of data, including:

Example: If you have the following list of numbers: [1, 2, 3, 4, 5], the arithmetic mean would be calculated like this:

(1 + 2 + 3 + 4 + 5) / 5 = 3

So, the mean value in this case is 3.

In Python, you can calculate the arithmetic mean using the statistics.mean() function. For example:

import statistics
numbers = [1, 2, 3, 4, 5]
mean_value = statistics.mean(numbers)
print(mean_value)  # Output: 3.0

Example: If you have the following list of numbers: [1, 2, 4], the geometric mean would be calculated like this:

√(124) = √8 ≈ 2.83

So, the geometric mean value in this case is approximately 2.83.

Example: If you have the following list of numbers: [1, 2, 3, 4, 5], the median would be:

[1, 2, 3, 4, 5].sort() -> [1, 2, 3, 4, 5]

median_value = (list[2]) # Output: 3

So, the median value in this case is 3.

In Python, you can calculate the median using the statistics.median() function. For example:

import statistics
numbers = [1, 2, 3, 4, 5]
median_value = statistics.median(numbers)
print(median_value)  # Output: 3.0

When to use mean?

You can use the mean (arithmetic or geometric) when:

On the other hand, you might want to consider using median instead of mean in certain situations:

In summary, the mean function in Python is used to calculate the arithmetic mean (average) of a set of numbers. It can be useful when you want a single value that represents the overall center of your data, but it's not always the best choice, depending on the nature of your data and what you're trying to achieve.