Python binary search api

Python binary search api

Python Binary Search API

In this article, we will explore the concept of binary search and its implementation as a Python API. The binary_search API takes a sorted list and an item to find as inputs and returns the index of the item if it exists in the list or -1 if it does not.

What is Binary Search?

Binary search is a fast search algorithm that finds the position of a target value within a sorted array. It works by repeatedly dividing the search interval in half until the target value is found. This algorithm has an average time complexity of O(log n), where n is the number of elements in the array.

Implementing Binary Search in Python

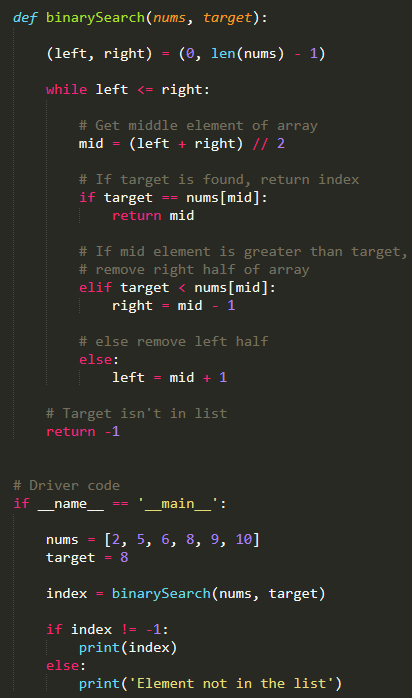
Here's the implementation of the binary search API using Python:

def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1

In the above implementation, we initialize two pointers: low and high. These pointers represent the search interval. We then calculate the midpoint of the search interval using the formula (low + high) // 2.

If the value at the midpoint is equal to the target, we return the index of the midpoint. If the value at the midpoint is less than the target, we update low to be the midpoint plus one. Otherwise, we update high to be the midpoint minus one.

We repeat this process until low is greater than high, which indicates that the target is not present in the list. In this case, we return -1.

Using the Binary Search API

To use the binary search API, you need to first create a sorted list of items. Here's an example:

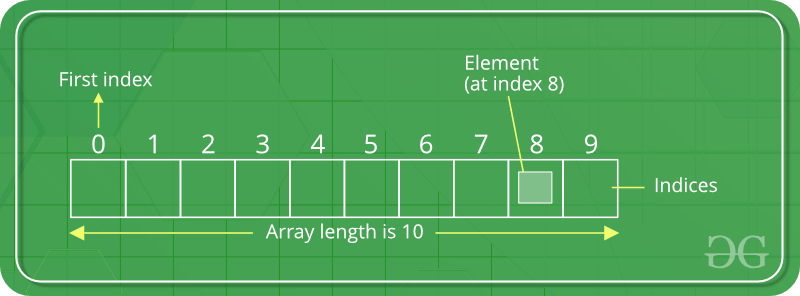
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]

Then, call the binary_search function with the list and the target item as inputs:

result = binary_search(arr, 5)
print(result)  # Output: 4

In this example, the binary_search API returns 4, which is the index of the item 5 in the sorted list. If you call the function with a target that does not exist in the list, it will return -1.

Advantages and Limitations

The binary search algorithm has several advantages:

However, there are some limitations:

Conclusion

In this article, we have implemented a binary search API in Python and discussed its advantages and limitations. Binary search is an efficient algorithm for finding items in sorted lists, but it requires that the input list be sorted and can only be used on lists or arrays.

Python binary search example

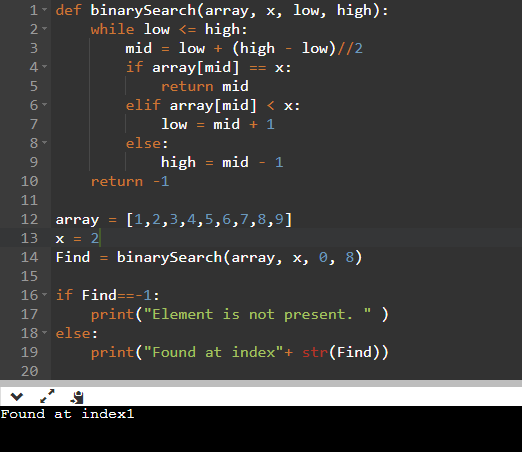
Here is an example of a Python program that uses the binary search algorithm to find a target value in a sorted list:

def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
Test the function
arr = [1, 3, 5, 7, 9]
target = 8
result = binary_search(arr, target)
if result != -1:
print("Target value found at index", result)
else:
print("Target value not found in the array")

This program defines a function called binary_search that takes two parameters: arr, which is the sorted list to search through, and target, which is the value we are trying to find. The function uses the binary search algorithm to efficiently search for the target value.

The algorithm starts by initializing two variables: low and high. These variables represent the range of indices in the array that we should consider searching within. Initially, this range is set to be the entire array (i.e., from index 0 up to and including the last index).

Next, the function calculates the midpoint of the current range using the expression (low + high) // 2. This is a simple way to calculate the midpoint without worrying about integer division.

The function then checks whether the value at the midpoint index matches the target value. If it does, the function returns the index of the target value.

If the value at the midpoint index is less than the target value, this means that the target value must be located in the upper half of the current range. In this case, we update the low variable to be equal to the midpoint index plus 1, effectively moving the lower bound of our search range up one step.

On the other hand, if the value at the midpoint index is greater than the target value, this means that the target value must be located in the lower half of the current range. In this case, we update the high variable to be equal to the midpoint index minus 1, effectively moving the upper bound of our search range down one step.

This process continues until we find the target value (in which case we return its index) or until the range is empty (in which case we conclude that the target value was not found in the array).

The test at the end of the program uses this binary_search function to search for the value 8 in a sample sorted list.