Python heapq peek

Python heapq peek

I'll respond in English as per your request.

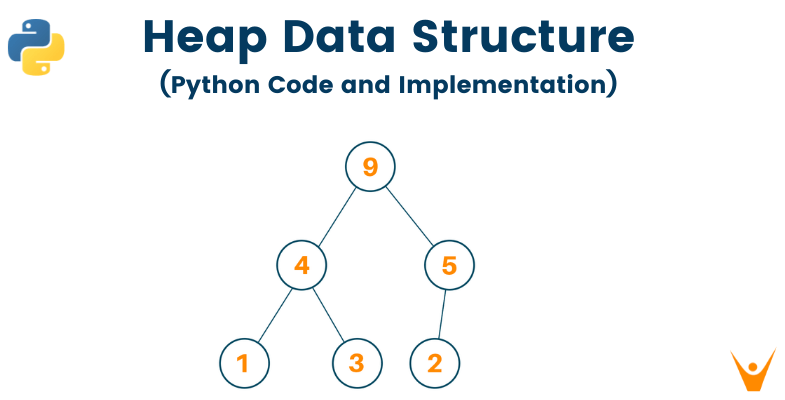
Python's heapq module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm. A heap is a specialized tree-based data structure that satisfies the heap property: the parent node is either greater than (in a max heap) or less than (in a min heap) its child nodes.

The heapq module offers several useful functions for creating and manipulating heaps:

Now, let's talk about peek. The peek method is used to get the top element from the heap without removing it. This operation does not modify the heap.

Here are some examples of using these functions:

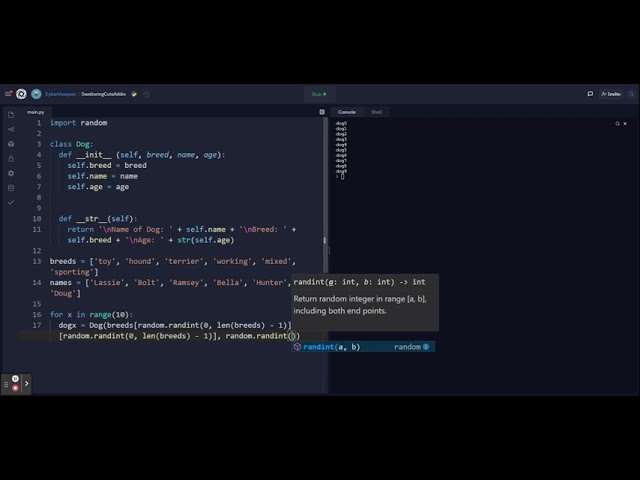
import heapq
Create a min-heap
min_heap = []
Add elements to the heap
heapq.heappush(min_heap, 5)
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 8)
Check the smallest element (peek)
print(heapq.nsmallest(1, min_heap))  # Output: [3]
Remove and return the smallest item
print(heapq.heappop(min_heap))  # Output: 3
Replace the smallest item with a new one
heapq.heapreplace(min_heap, 4)
Check the heap again (peek)
print(heapq.nsmallest(1, min_heap))  # Output: [4]

In this example, we first create an empty min-heap and then push several elements onto it. We use nsmallest to get the smallest element from the heap without removing it. Then, we pop and return the smallest item using heappop. Finally, we replace the smallest item with a new one using heapreplace.

The peek operation in this context allows us to inspect the top element of the heap without modifying it. This is particularly useful when you need to decide whether to remove an element or not based on its value.

Remember that peek does not modify the heap, so we can safely use it multiple times without affecting the ordering of the elements.

Is Python heapq min or max?

I'm happy to respond in English for this question.

Python's heapq module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm. The fundamental difference between a min-heap and a max-heap is how they order their elements based on some criteria, typically referred to as the "priority" or "value".

A min-heap is a complete binary tree where each node's key (or value) is less than or equal to its children's keys. This means that the smallest element in the heap is always at the root, and the largest elements are located at the leaves.

In contrast, a max-heap is also a complete binary tree where each node's key is greater than or equal to its children's keys. Here, the largest element resides at the root, while the smallest ones are situated at the leaves.

Python's heapq module provides two main functions: heappush() and heappop(). These functions allow you to add elements to a min-heap (which is the default behavior) or max-heap. The heappush() function adds an element to the heap, maintaining the heap invariant, while the heappop() function removes and returns the smallest or largest element from the heap, depending on whether you're working with a min-heap or max-heap.

To create a max-heap using heapq, you need to pass nlargest=True as an argument when calling the nsmallest() or nsample() functions. For example:

import heapq
Create a list of numbers
numbers = [4, 2, 9, 6, 23, 12, 34, 1]
Convert the list into a max-heap
max_heap = []
for num in numbers:
heapq.heappush(max_heap, -num)  # Note the minus sign!
print("Max heap:", max_heap)
while max_heap:
print(heapq.heappop(max_heap))

In this example, we create a list of numbers and then convert it into a max-heap by pushing each element onto the heap with a minus sign in front. This is because heapq's default behavior is to create a min-heap, so by negating the values, we effectively create a max-heap.

When you run this code, it will print out the elements of the original list in descending order, which corresponds to the expected ordering for a max-heap.